1.个人完成情况_____

2.教学与测试，测试反馈相对应作业。

[完成预习案情况]

1.上作业本作业：课本P28 (2) (3) (4) (5)

2.a=6,c=1,焦点在y轴上的椭圆的标准方程　　　　　　

2判定下列椭圆的标准方程在哪个轴上，并写出焦点坐标。

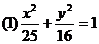
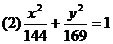
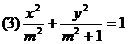
(3)已知椭圆的方程为：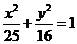　　 　　　　　　　　　　

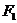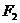
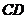则a=_____，b=_______，c=_______，焦点坐标为：____________焦距等于______;若CD为过左焦点的弦，则△的周长为________

(4)椭圆　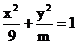 　的焦距为4, 则 m 的值为：　　　　

解题感悟

[预习提高题]

1已知椭圆焦点的坐标分别是(-4,0)、(4,0)，椭圆上一点P到两焦点的距离的和等于10，求椭圆的标准方程

2平面内两个定点的距离是8 ，求到两个定点距离的和是10的点的轨迹

3过椭圆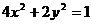的一个焦点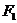的弦AB与另一焦点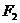围成的△的周长是　　　　

题后小结

[教师精讲点拨例题]

例1 已知椭圆的两个焦点的坐标分别是 (0 ,-2)(0 ,2)并且经过点　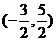 　　求椭圆的标准方程

例2：若方程4x²+kx²=1表示的曲线是焦点在y轴上的椭圆，求k的取值范围。

例3方程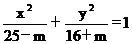　　　　　　　　　　　　　

分别求方程满足

下列条件的m的取值范围：

①表示一个圆；

②表示一个椭圆；

③表示焦点在x轴上的椭圆。

_

解题感悟

[课堂展示]

(1)两个焦点分别是F1(－2,0)、F2(2,0),且过P(2,3)点；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(2)已知B、C是两个定点，︱BC︱=6，且△ABC的周长等于16，求顶点A的轨迹方程。

[课后作业]

1.在方程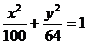中，a=　　　　

b=　　　　　 　c=　　　　　　

2.《教学测试》6双基演练

[课本梳理]

1 椭圆的定义　　　　　　　　　　　　　　　

⑴若2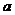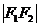＞，则动点P的轨迹是　　

⑵若2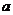=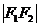，则动点P的轨迹是　　　　

⑶若2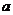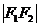＜，则动点P 　　　　　　

2椭圆的标准方程

焦点在轴上时，方程为 　　　　　　　　

焦点坐标　　 　　　　　　　　　　

焦点在y轴上时，方程为 　　　　　　　　

焦点坐标　　　　　　　　　　　

以上两种方程都称为　　　　　　　　　　

这里　 　　　　　　　　　　　　　　　　　　　　　　　　　　　

3推导椭圆的标准方程(课本P26)

求轨迹方程的一般步骤:　　　　　　

(1) 建系设点 (2) 写出点的集合

(3)写出代数方程　 (4) 化简方程　

(5)证明

[联系生活]

情境1.生活中,你见过哪些类似椭圆的图形或物体?

情境2.观察倾斜的圆柱形水杯的水面边界线，并从中抽象出数学模型

[预习检测]

1.课本P26-28

2.2．1椭圆的标准方程

★[学习目标]1准确理解椭圆的定义,掌握椭圆的标准方程及其推导.

2通过学生亲自动手尝试画图、发现椭圆的形成过程进而归纳出椭圆的定义,培养学生观察、辨析、归纳问题的能力

★[学习内容]

2.互助小组的合作探究情况______

①很好　 ②较好　 ③一般　 ④较差

1.个人完成情况_____