
1.上作业本作业:书P84习题2.1(2) 2
4.已知直线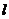 和直线
和直线
 垂直,且与
垂直,且与 在
在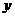 轴上的截距相同,求直线
轴上的截距相同,求直线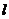 的方程。
的方程。
3.若直线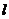 在
在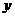 轴上的截距为2,且与直线
轴上的截距为2,且与直线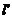
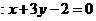 垂直,求直线
垂直,求直线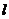 的方程。
的方程。
2.原点在直线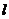 上的射影是
上的射影是 ,则
,则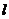 的方程是_____________________
的方程是_____________________
1.过点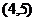 且与原点距离最远的直线的方程是_____________________
且与原点距离最远的直线的方程是_____________________
例1(1)已知四点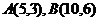
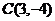
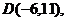 求证:
求证: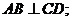
解:由斜率公式,得 则有 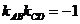 ,则 ,则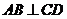 |
(2)已知直线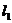 的斜率
的斜率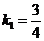 ,经过点
,经过点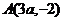 ,
,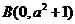 且
且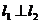 ,求实数
,求实数 的值。
的值。
解:由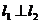 可知 可知 即 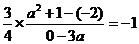 解得 解得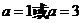 |
例2、已知三角形的顶点A(2,4),B(1,-2),
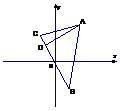 C(-2,3),求BC边上的高AD所在的直线方程.
C(-2,3),求BC边上的高AD所在的直线方程.
|
解题方法:利用 高即是垂直。 解:直线BC的斜率为  因为AD⊥BC, 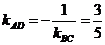 根据点斜式,得所求直线方程为 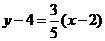 即 即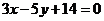 |
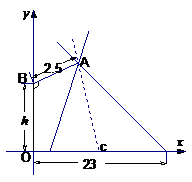 例3、在路边安装路灯,路宽23m,灯杆长2.5,且与灯柱成120°角,路灯采用锥形灯罩,灯罩轴线与灯杆垂直。当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)
例3、在路边安装路灯,路宽23m,灯杆长2.5,且与灯柱成120°角,路灯采用锥形灯罩,灯罩轴线与灯杆垂直。当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01m)
  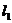 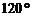 解:如图,记灯柱顶端为 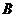 ,灯罩顶为 ,灯罩顶为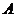 ,灯杆为 ,灯杆为 ,灯罩轴线与道路中线交于点 ,灯罩轴线与道路中线交于点 ,以灯柱底端点 ,以灯柱底端点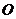 为原点,灯柱 为原点,灯柱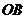 为 为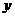 轴,建系如图。 轴,建系如图。 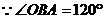  直线 直线 的倾斜角为 的倾斜角为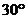 则  即 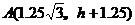 因为CA⊥BA, 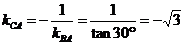 得CA的方程: 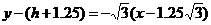 将C点代入方程得: 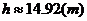 答: |
补例:已知直线 与
与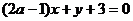 互相垂直,求
互相垂直,求 的值。
的值。
解:由 解得 解得 (1)当 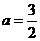 时,两方程 时,两方程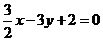 与 与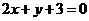 互相垂直。 互相垂直。(2)当 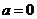 时,第一条直线方程不成立,舍去。 时,第一条直线方程不成立,舍去。所以 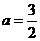 总结方法: 总结不足: |
1.判断下列两直线是否垂直,并说明理由.
(1) 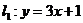

|
垂直 |
(2) 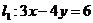
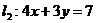
|
垂直 |
(3) 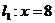

|
垂直 |
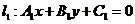 其中
其中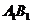 不全为0
不全为0
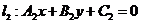 其中
其中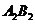 不全为0
不全为0
当 时,
时, 有怎样的关系?
有怎样的关系?
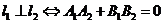
如果两条直线中的一条斜率不存在,那么这两条直线什么时候垂直?
|
另一条直线的斜率为0时 |
2.互助小组的合作探究情况______
①很好 ②较好 ③一般 ④较差
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com