2.　　　 在yoz面上，有一点M与三个已知点A(3,1,2),B(4,-2,-2)和C(0，5，1)等距离，求点M的坐标. (答案见测试反馈)

1.　　　 已知球心M(1,1,2),球的一条直径的一个端点为A(-1，2，2)，求该直径另一个

端点的坐标，球的表面积，球面上任一点的轨迹方程。(答案见测试反馈)

2．Xoy坐标平面内的点的竖坐标为0，横坐标与纵坐标分别是点向两轴作垂线交点的坐标

典型例题3.(1)在空间直角坐标系o-xyz中，画出不共线的3个点P,Q,R,使得这3个点的坐标都满足z=3，并画出图形。

(2)写出由这三个点确定的平面内的点坐标应满足的条件．(答案见课本)

新知5：空间任意两点A(x1,y1,z1),P(x2,y2,z2)间的距离

典型例题4：求空间两点A(3，－2，5)，B(6，0，－1)的距离AB(答案见课本)

练习1：P(1,2,-2)和Q(-1,0,-1)的距离是3

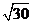练习2：给定空间直角坐标系，在x轴上找一点P，使它与点P (4,1,2) 距离为

典型例题5：在xoy平面内的直线x+y=1上确定一点M，使M到N(6,5,1)的距离最小

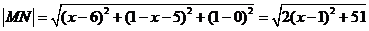
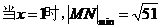
典型例题6：.平面上到坐标原点的距离为1的点的轨迹是单位圆，其方程为　　　　　　　　　　　　　　　 ．

　在空间中，到坐标原点的距离为1的点的轨迹是什么？试写出它的方程(答案见课本)

新知6：已知点A(x1,y1,z1),点B(x2,y2,z2)，则线段AB中点C的坐标是

典型例题7：设A(3,3,1),B(1,-1,5),C(0,1,0),则AB的中点M到C的距离为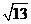

典型例题8：已知P(2,-2,3)

(1)　　 求P关于原点的对称点坐标(2)求P关于x轴的对称点坐标

(-2，2，-3)　　　　　　　　　　 (2，2，-3)

学习反思2：写出对称点的坐标(无哪个轴的坐标变号)；

★　　 自主检测

1．X轴上的点横坐标就是与x轴交点的坐标，纵坐标和竖坐标都是0．

2.y轴和z轴的单位长度相同，x轴上的单位长度为y轴(或z轴)的单位长度的一半．

新知4：空间任意一点的坐标的含义

经过A点作三个平面分别垂直于x轴、y轴和z轴，它们与x轴、y轴和z轴分别交于三点，三点在相应的坐标轴上的坐标a,b,c组成的有序实数对(a,b,c)叫做点A的坐标记为：A(a,b,c)

典型例题1：在空间直角坐标系中，作出点(5,4,6).

(答案见课本)

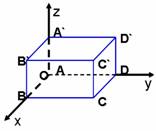
典型例题2：如图，已知长方体ABCD-A`B`C`D`的边长为AB=12,AD=8,AA`=5.以这个长方体的顶点A为坐标原点，射线AB,AD,AA`分别为x轴、y轴和z轴的正半轴,建立空间直角坐标系,求长方体各个顶点的坐标．(答案见课本)

学习反思1：在空间直角坐标系中,x轴上的点、xoy坐标平面内的点的坐标各有什么特点？

1.X轴与y轴、x轴与z轴均成1350,而z轴垂直于y轴．