1.通过预习我已掌握：_________________

____________________________________

4．已知通过点A(－3，5)的一束光线遇直线l:3x－4y+4＝0后反射，如果反射光线通过点B(2，15)，试求反射光线所在直线方程

学习小结：

3．试用解析几何的方法证明直角三角形斜边中线等于斜边的一半．

2．已知△ABC的顶点坐标为A(－1，5)，B(－2，－1)，C(4，7)，求BC边上的中线AM的长和AM所在的直线方程．

1．已知A，B两点都在直线y＝2x+1上，且A，B两点的横坐标之差为，A，B两点之间的距离为__________．

2．点P(x，y)关于M(a，b)的对称点P′(x′，y′)的坐标：__________________

例1：已知点A(1，2)，B(3，1)，则线段AB的垂直平分线的方程是______________

练习1：已知矩形ABCD两个顶点A(－1，3)，B(－2，4)，若它的对角线交点M在x轴上，求C，D两点的坐标．

练习2：过点P(3，0)作直线l，使它被直线l1:2x－y－2＝0，l2:x+y+3＝0所截得的线段AB恰好被P所平分，求此直线l方程．

新知3

对称问题

例：已知直线l:y＝x－1．

(1)求点P(3，4)关于l对称的点Q；

(2)求l关于点(2，3)对称的直线方程．

课堂练习：

1．对于平面上的两点P₁(x₁，y₁)， P₂(x₂，y₂)，线段P₁P₂的中点是M(x₀，y₀)，则_____________________

2．y轴上两点P₁(0，y₁)， P₂(0，y₂)的距离| P₁P₂|＝___________

若两点连线与x轴平行，两点间距离怎么算？

若两点连线与y轴平行，两点间距离怎么算？

推广： P₁(x₁，a)， P₂(x₂，a)的距离| P₁P₂|＝_______________

P₁(0，y₁)， P₂(0，y₂)的距离| P₁P₂|＝_______________

P₁(a，0)， P₂(0，b₂)的距离| P₁P₂|＝_______________．

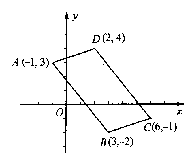
已知A(－1，3)，B(3，－2)，C(6，－1)，D(2,4),四边形ABCD是否为平行四边形？

　　　　 一般地已知两点P₁(x₁，y₁)， P₂(x₂， y₂)，如何求P_1, P₂两点间的距离呢？

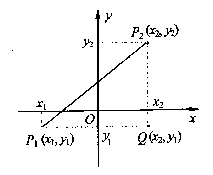
如果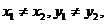过P_1，P₂ 分别向y轴，x轴作垂线，两条垂线交于点Q，则点Q的坐标为(x₂，y₁)

因为P₁Q=| x₂－x₁ |, P₂Q=|y₂－y₁ |,

所以在Rt△P₁ P₂Q中，

__________________________

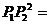新知1

平面上两点间的距离公式．

平面上两点P₁(x₁，y₁)， P₂(x₂，y₂的距离| P₁P₂|＝．

　 (读书)：(1)求A(1，3)，B(2，5)两点间的距离　　　　　　　

　　　　　 (2)已知A(0，10)，B(a，－5)两点的距离是17，求实数a的值．　

例1：已知点A(1，2)，B(2，)，试在x轴上求一点P，使PA＝PB，并求此时PA的值．

练习1：已知过点A(4，a)和B(5，b)的直线与直线y＝x+m平行，则|AB|的值为_____________．

练习2：求函数f(x)＝+的最小值．

解题反思：此函数的定义域为R，如果从代数的角度考虑，确实比较复杂；如果借助于两点间的距离公式，转化为几何问题，则非常容易。解决问题的关键是_________________,进而求解。

新知2

中点坐标公式．

1．x轴上两点P₁(x₁，0)， P₂(x₂，0)的距离| P₁P₂|＝___________

4.新课内容:课本第85到89页

如何求平面上两点间的距离？平面上两点在x轴上距离怎么算？平面上两点在y轴上距离怎么算？