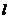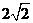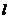4.直线平行于直线x－y－2=0，且两直线的距离为，则直线的方程为__________

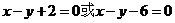
3.直线6x－4y+5=0与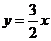间的距离____

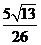
2.已知x轴上一点P到直线3x+4y－6=0的距离为4，则点P的坐标为_______________

问题 建立适当的坐标系，证明：等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高.

已知：

求证：

证明：(建立适当的坐标系，设出点的坐标)

(求出直线AB,BC的方程)

(求出P到AB，P到BC，A到BC的距离)

(得出结论)

题后小结建立坐标系是将几何问题转化为代数问题的基础(解析法)；建立合理的坐标系能减少解题运算量；一般步骤：(1)建系设点；(2)列式；(3)求解.

[基础训练]

1.点P(－2，1)到直线3y+5=0的距离______

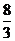
2.两平行线间的距离

(1)尝试求两条平行直线x+3y－4=0与2x+6y－9=0之间的距离.

简解：在x+3y－4=0上取点(4，0)，利用点到直线的距离公式求得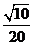

题后小结

将两平行线距离问题化归为点到直线距离问题

(2)推导两平行直线间距离公式

已知

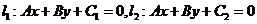
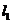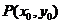在上任取点，则点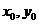满足_____________,又点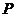到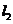的距离可表示为_________________,消去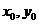后得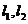间的距离为___________________________

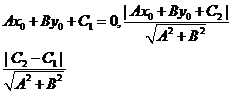
(3)试用推导出的公式求解(1)中的问题

题后小结

直线方程要化成一般式，x，y前的系数要相同.

1.点到直线的距离公式

点___________到直线__________________

的距离为d=___________________________

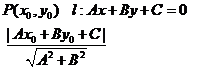
特别的：当直线与x轴垂直时，点________

到直线_________的距离是______________

当直线与y轴垂直时，点_________________

到直线_________的距离是______________

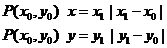
练习：求点P(－1，2)到下列直线的距离：

(1)2x+y=10

(2)3x－2=0

题后小结(使用公式的注意点)

直线方程一定要化成一般式，特殊情况特殊处理

(1)________________________________求垂足坐标，用两点间距离公式

(2)________________________________三角形中等积法求距离

建议：

(1)自己动手重现课本上的求解过程；

(2)思考还可怎样求该平行四边形面积？

用向量求夹角，体现化归思想

(3)还能想到其他推导点到直线距离公式的方法吗？

比如(2)的向量的方法

4.我的建议：________________________

____________________________________

_____________________________________

3.我需要老师重点讲解的问题是：_______

_____________________________________

2.我还有没解决的问题是：_____________

_____________________________________