
2、直线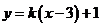 恒过点
。
恒过点
。
通过预学,我懂得了:
第 组的问题是:
※学习评价
◆自我评价 完成本节预学案的情况是()
A.很好 B较好 C一般 D不理想
◆自我检测
1、过点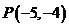 ,倾斜角为
,倾斜角为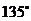 的直线方程是
。
的直线方程是
。
2. 已知直线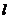 经过点
经过点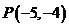 ,且直线与两坐标轴围成的三角形面积为5,求直线
,且直线与两坐标轴围成的三角形面积为5,求直线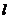 的方程。
的方程。
★学习探究
问题1:在直角坐标系内确定一条直线,应知道那些条件?
新知1:已知斜率为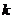 的直线
的直线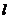 经过
经过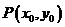 ,则方程
,则方程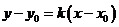 为直线的点斜式方程
为直线的点斜式方程
问题2:直线的点斜式方程能否表式坐标平面上的所有直线呢?
问题3:
(1)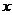 轴所在直线的方程是 ,
轴所在直线的方程是 ,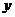 轴所在直线的方程是 。
轴所在直线的方程是 。
(2)经过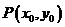 且平行于
且平行于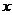 轴的直线方程
,经过
轴的直线方程
,经过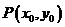 且平行于
且平行于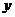 轴的直线方程
。
轴的直线方程
。
问题4:已知直线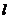 的斜率为
的斜率为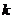 ,且与
,且与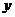 轴交点为
轴交点为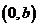 ,求直线
,求直线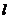 的方程。
的方程。
新知2:直线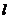 与
与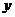 轴交点
轴交点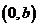 的纵坐标
的纵坐标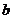 叫做直线在
叫做直线在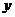 轴上的截距,方程
轴上的截距,方程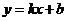 叫做直线
叫做直线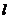 的斜截式方程。
的斜截式方程。
注:直线在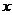 轴上截距就是直线与
轴上截距就是直线与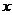 轴交点的横坐标。
轴交点的横坐标。
问题5:能否用斜截式表式平面内所有直线?斜截式与我们学过的一次函数表达式比较你会得出什么结论?
★ 典型例题
例1.
直线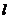 经过
经过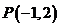 ,且倾斜角为
,且倾斜角为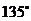 ,求直线
,求直线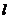 的点斜式方程和斜截式方程。
的点斜式方程和斜截式方程。
变式:
(1)直线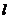 经过
经过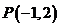 ,且平行于
,且平行于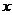 轴的直线方程
。
轴的直线方程
。
(2)直线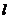 经过
经过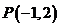 ,且平行于
,且平行于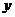 轴的直线方程
。
轴的直线方程
。
(3)直线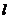 经过
经过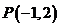 ,且过原点的直线方程
。
,且过原点的直线方程
。
例2.写出下列直线的斜截式方程:
(1) 斜率是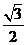 ,在
,在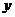 轴上的截距是-2;
轴上的截距是-2;
(2) 倾斜角为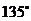 ,在
,在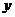 轴上的截距是0.
轴上的截距是0.
变式:已知直线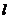 的方程为
的方程为 ,求直线
,求直线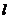 的斜率及纵截距。
的斜率及纵截距。
★ 能力提升
1. 将直线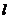 :
: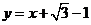 绕其上一点
绕其上一点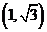 沿逆时针方向旋转
沿逆时针方向旋转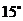 ,求所得新的直线方程。
,求所得新的直线方程。
3、直线的倾斜角和斜率有何关系?什么样的直线没有斜率?
2、已知长方形ABCD的三个顶点坐标分别为A(0,1),B(1,0),C(3,2),则第四个顶点D的坐标 。
1、若三点A(3,1),B(-2,k),C(8,11)在同一条直线上,则k= .
6.已知点P(2,-1),求:
(1) 过点P与原点距离为2的直线的方程;
(2)过点P与原点距离最大的直线方程,并求出最大距离;
(3)是否存在过P点与原点距离为6的直线?若存在,求出直线方程;若不存在,说明理由.
题后小结
[问题反馈]
5.已知△ABC的三个顶点坐标分别为A(3,4),B(6,0),C(-5,-2),求∠A的平分线AT所在的直线方程和角平分线AT的长.
4.到两条平行直线2x+y+1=0和2x+y+5=0的距离相等的点的轨迹方程是_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com