2.　　　 用数形结合思想分析斜率的概念，并解释生活中的某些现象。

★学习过程

▲问题情景

(1)_________确定一条直线

(2)过一个点有___________条直线

确定直线位置的要素除了点之外，还有直线的方向，也就是直线的倾斜程度

▲建构数学

直线斜率的定义__________________________________________________

▲数学实践：请你任意给出两个点的坐标，并让同组的成员求出这两点的直线的斜率。

▲概念辩析：

1.　　　 理解直线斜率的概念，掌握直线斜率的坐标公式，会求已知直线的斜率。

3.　　　 直线l过点M(-1，1)且与以P(-2，2)，Q(3，3)为两端点的线段PQ有公共点，求直线l的斜率的取值范围。

2.　　　 教学与测试，测试反馈。

1.　　　 结合预学案和课堂学习情况整理笔记

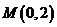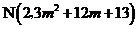5.求过点和的直线l的斜率k的取值范围

　　　　 K》-1/2

　▲思考：直线斜率的大小与直线的倾斜程度有什么联系？

▲问题情景：

在直角坐标系中，任何一条直线与X轴都有一个相对倾斜度，可以用一个什么几何量来反映一条直线与X轴的相对倾斜程度呢？

△定义_____________________________________

△倾斜角的范围_________________

△思考：任何一条直线都有倾斜角吗？不同的直线其倾斜角一定不相同吗？

　　　　　　 是，否

▲数学应用：

△函数y=x,y=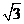x的图像是直线，这两条直线的倾斜角分别是多少？

　 △上述两条直线的倾斜角分别与x的系数有什么关系？

△斜率与倾斜角之间的关系______________

▲思考：

　　 △当倾斜角为锐角，钝角的直线的斜率的取值范围分别是什么？

　　 △一般地，直线的斜率的取值范围是什么？

　　 △斜率相等的直线其倾斜角相等吗？　 斜率大的直线其倾斜角也大吗？

▲数学应用：

　 已知点A(3，2)，B(-4，1)，C(0，-1)，求直线AB,BC,CA的斜率，并判断这些直线的倾斜角是锐角还是钝角？

▲学习小结：

▲　　 课后作业：

4.已知三点A(-3，-3)，B(-1，1)，C(2，7)，求KAB=_2_____,KBC=__2____

　 　问题：△如果KAB=KBC,那么A,B,C三点有怎样的位置关系？

　　　　　　 三点共线

　　　 　△如果三点A(1，1)，B(3，5)，C(-1，a)在一条直线上，求a的值。

　　　　　　 a=-3

3.斜率为2的直线，经过点(3，5)，(a，7)，(-1，b)三点，则a,b的值为_4,-3_____

2.已知点P(2，3)，点Q在y轴上，若直线PQ的斜率为1，则点Q的坐标为______(0,1)_____

1.已知直线l经过点P(2，3)与Q(-3，2)则直线的斜率为___1/5_________