
[名师点睛]函数零点的概念对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点
方程f(x)=0有实数根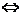 函数y=f(x)的图象与x轴有交点
函数y=f(x)的图象与x轴有交点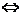 函数y=f(x)有零点
函数y=f(x)有零点
连续函数在某个区间上存在零点的判别方法:如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.
[试题演练]
1、函数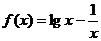 的零点所在的区间是
的零点所在的区间是
A.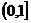 B.(1,10) C.
B.(1,10) C.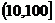 D.
D.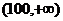
解:因为f(1)=0-1<0,f(10)=1-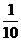 >0,即f(1)•f(10)<0,所以函数f(x)在区间(1,10)之间有零点。
>0,即f(1)•f(10)<0,所以函数f(x)在区间(1,10)之间有零点。
[点评]:如果函数f(x)在区间[a,b]上连续,且f(a)•f(b)<0,则函数f(x)在区间(a,b)上有零点,函数的零点,二分法,函数的应用都是函数的重点内容。
2、某商品每件成本9元,售价为30元,每星期卖出432件. 如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值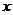 (单位:元,
(单位:元,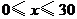 )的平方成正比.已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成
)的平方成正比.已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成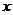 的函数;(II)如何定价才能使一个星期的商品销售利润最大?
的函数;(II)如何定价才能使一个星期的商品销售利润最大?
本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.
[解析]:(Ⅰ)设商品降价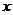 元,则多卖的商品数为
元,则多卖的商品数为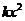 ,若记商品在一个星期的获利为
,若记商品在一个星期的获利为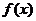 ,则依题意有
,则依题意有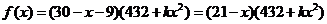 ,又由已知条件,
,又由已知条件,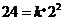 ,于是有
,于是有 ,所以
,所以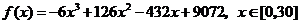 .
.
(Ⅱ)根据(Ⅰ),我们有 .
.
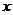 |
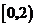 |
2 |
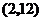 |
12 |
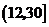 |
 |
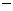 |
0 |
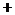 |
0 |
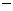 |
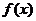 |
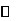 |
极小 |
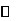 |
极大 |
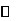 |
故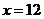 时,
时,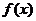 达到极大值.因为
达到极大值.因为 ,
, ,所以定价为
,所以定价为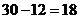 元能使一个星期的商品销售利润最大.
元能使一个星期的商品销售利润最大.
[点评]:本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.
[名师点睛]函数的综合运用主要是指运用函数的知识、思想和方法综合解决问题.函数描述了自然界中量的依存关系,是对问题本身的数量本质特征和制约关系的一种刻画,用联系和变化的观点提出数学对象,抽象其数学特征,建立函数关系.因此,运动变化、相互联系、相互制约是函数思想的精髓,掌握有关函数知识是运用函数思想的前提,提高用初等数学思想方法研究函数的能力,树立运用函数思想解决有关数学问题的意识是运用函数思想的关键.
[试题演练]
1、某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算,如果将楼房建为x(x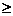 10)层,则每平方米的 平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
10)层,则每平方米的 平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
[解析]:设楼房每平方米的平均综合费为 元,依题意得
元,依题意得
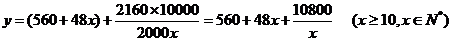
则 ,令
,令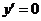 ,即
,即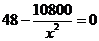 ,解得
,解得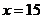
当 时,
时,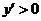 ;当
;当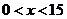 时,
时,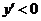 ,
,
因此,当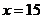 时,
时, 取得最小值,
取得最小值,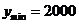 元.
元.
答:为了使楼房每平方米的平均综合费最少,该楼房应建为15层。
[点评]:这是一题应用题,利用函数与导数的知识来解决问题。利用导数,求函数的单调性、求函数值域或最值是一种常用的方法.
(一) 函数性质法
函数的特征是通过其性质(如奇偶性,单调性周期性,特殊点等)反应出来的,抽象函数也是如此,只有充分挖掘和利用题设条件和隐含的性质,灵活进行等价转化,抽象函数问题才能转化,化难为易,常用的解题方法有:1,利用奇偶性整体思考;2,利用单调性等价转化;3,利用周期性回归已知4;利用对称性数形结合;5,借助特殊点,布列方程等.
(二 )特殊化方法
1、在求解函数解析式或研究函数性质时,一般用代换的方法,将x换成-x等2、在求函数值时,可用特殊值代入3、研究抽象函数的具体模型,用具体模型解选择题,填空题,或由具体模型函数对综合题,的解答提供思路和方法.
总之,抽象函数问题求解,用常规方法一般很难凑效,但我们如果能通过对题目的信息分析与研究,采用特殊的方法和手段求解,往往会收到事半功倍之功效,真有些山穷水复疑无路,柳暗花明又一村的快感.
[试题演练]
1、定义在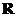 上的函数
上的函数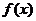 满足
满足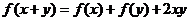 (
(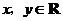 ),
),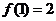 ,则
,则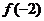 等于( )
等于( )
A.2 B.3 C.6 D.9
解:令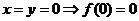 ,令
,令 ;
;
令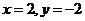 得
得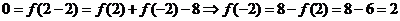
2、
解: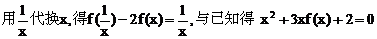
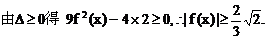
3、已知函数f(x)对任何正数x,y都有f(xy)=f(x)f(y),且f(x)≠0,当x>1时,f(x)<1.试判断f(x)在
(0,+∞)上的单调性,并说明理由.
解: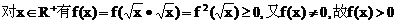
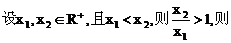
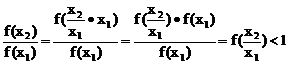
所以f(x1)>f(x2),故f(x)在R+上为减函数
4、设定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意x,y∈R,有f(x+y)=f(x)f(y),f(1)=2

解:(1)先证f(x)>0,且单调递增,因为f(x)=f(x+0)=f(x)f(0),x>0时f(x)>1,所以f(0)=1.
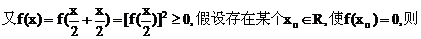 f(x)=f[(x-xo)+xo]=f(x-xo)f(xo)=0,与已知矛盾,故f(x)>0任取x1,x2∈R且x1<x2,则x2-x1>0,f(x2-x1)>1,所以f(x1)-f(x2)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]>0.所以x∈R时,f(x)为增函数. 解得:{x|1<x<2}
f(x)=f[(x-xo)+xo]=f(x-xo)f(xo)=0,与已知矛盾,故f(x)>0任取x1,x2∈R且x1<x2,则x2-x1>0,f(x2-x1)>1,所以f(x1)-f(x2)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]>0.所以x∈R时,f(x)为增函数. 解得:{x|1<x<2}
(2)f(1)=2,f(2)=2,f(3)=8,原方程可化为:[f(x)]2+4f(x)-5=0,解得f(x)=1或f(x)=-5(舍)由(1)得x=0.
[名师点睛]
抽象函数是指没有给出具体的函数解析式或图像,只给出一些函数符号及其满足的条件的函数,如函数的定义域,解析递推式,特定点的函数值,特定的运算性质等,它是高中函数部分的难点,也是大学高等数学函数部分的一个衔接点,由于抽象函数没有具体的解析表达式作为载体,因此理解研究起来比较困难.但由于此类试题即能考查函数的概念和性质,又能考查学生的思维能力,所以备受命题者的青睐,那么,怎样求解抽象函数问题呢,我们可以利用特殊模型法,函数性质法,特殊化方法,联想类比转化法,等多种方法从多角度,多层面去分析研究抽象函数问题.
2、设函数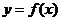 存在反函数
存在反函数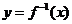 ,且函数
,且函数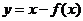 的图象过点(1,2),则函数
的图象过点(1,2),则函数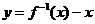 的图象一定过点 .
的图象一定过点 .
[解析]由函数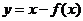 的图象过点(1,2)得:
的图象过点(1,2)得: 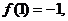 即函数
即函数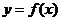 过点
过点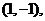 则其反函数过点
则其反函数过点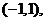 所以函数
所以函数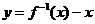 的图象一定过点
的图象一定过点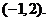
[点评]:本题考查互为反函数的两个函数的图象之间的关系以及图象的平移。
1、函数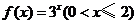 的反函数的定义域为( )
的反函数的定义域为( )
A.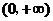 B.
B. C.
C.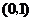 D.
D.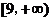
[解析]:函数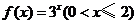 的反函数的定义域为原函数的值域,原函数的值域为
的反函数的定义域为原函数的值域,原函数的值域为 ,∴ 选B。
,∴ 选B。
[点评]:本题考查互为反函数的两个函数性质之间的关系,即:反函数的定义域为原函数的值域。
3.互为反函数的两个函数性质之间的关系:注意:在定义域内严格单调的函数必有反函数,但存在反函数的函数在定义域内不一定严格单调,如y=。
[试题演练]
2.互为反函数的两个函数的图象之间的关系,
[名师点睛]
反函数在高考试卷中一般为选择题或填空题,难度不大。通常是求反函数或考察互为反函数的两个函数的性质应用和图象关系。主要利用方法为:
1.反函数的概念及求解步骤:①由方程y=¦(x)中解出x=j(y);即用y的代数式表示x.。②改写字母x和y,得出y=¦-1(x);③求出或写出反函数的定义域,(亦即y=¦(x)的值域)。 即反解Þ互换Þ求定义域
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com