
10.(2009重庆卷文)记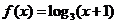 的反函数为
的反函数为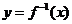 ,则方程
,则方程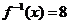 的解
的解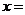 .
.
[答案]2
解法1由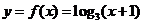 ,得
,得 ,即
,即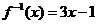 ,于是由
,于是由 ,解得
,解得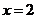
解法2因为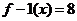 ,所以
,所以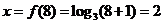
8.(2009山东卷理)已知定义在R上的奇函数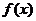 ,满足
,满足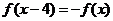 ,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间
,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间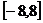 上有四个不同的根
上有四个不同的根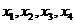 ,则
,则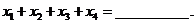
[解析]:因为定义在R上的奇函数,满足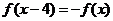 ,所以
,所以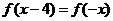 ,所以, 由
,所以, 由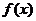 为奇函数,所以函数图象关于直线
为奇函数,所以函数图象关于直线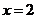 对称且
对称且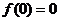 ,由
,由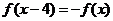 知
知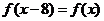 ,所以函数是以8为周期的周期函数,又因为
,所以函数是以8为周期的周期函数,又因为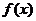 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以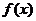 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间
在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间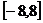 上有四个不同的根
上有四个不同的根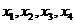 ,不妨设
,不妨设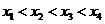 由对称性知
由对称性知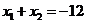
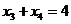 所以
所以
 答案:-8
答案:-8
[命题立意]:本题综合考查了函数的奇偶性,单调性,
对称性,周期性,以及由函数图象解答方程问题,
运用数形结合的思想和函数与方程的思想解答问题.
9(2009山东卷文)若函数f(x)=a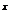 -x-a(a>0且a
-x-a(a>0且a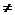 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 .
[解析]: 设函数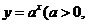 且
且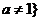 和函数
和函数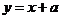 ,则函数f(x)=a
,则函数f(x)=a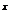 -x-a(a>0且a
-x-a(a>0且a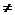 1)有两个零点, 就是函数
1)有两个零点, 就是函数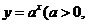 且
且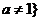 与函数
与函数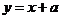 有两个交点,由图象可知当
有两个交点,由图象可知当 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当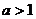 时,因为函数
时,因为函数 的图象过点(0,1),而直线
的图象过点(0,1),而直线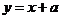 所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是 .
.
答案: 
[命题立意]:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答.
7.(2009山东卷理)若函数f(x)=a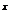 -x-a(a>0且a
-x-a(a>0且a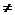 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 .
[解析]: 设函数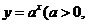 且
且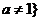 和函数
和函数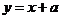 ,则函数f(x)=a
,则函数f(x)=a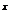 -x-a(a>0且a
-x-a(a>0且a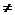 1)有两个零点, 就是函数
1)有两个零点, 就是函数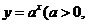 且
且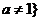 与函数
与函数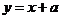 有两个交点,由图象可知当
有两个交点,由图象可知当 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当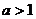 时,因为函数
时,因为函数 的图象过点(0,1),而直线
的图象过点(0,1),而直线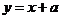 所过的点一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是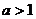
答案: 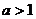
[命题立意]:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象解答.
6.(2009江苏卷)已知集合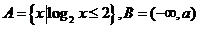 ,若
,若 则实数
则实数 的取值范围是
的取值范围是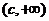 ,其中
,其中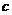 = .
= .
[解析] 考查集合的子集的概念及利用对数的性质解不等式。
由 得
得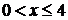 ,
,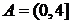 ;由
;由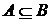 知
知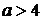 ,所以
,所以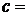 4。
4。
5.(2009江苏卷)已知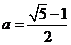 ,函数
,函数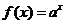 ,若实数
,若实数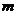 、
、 满足
满足 ,则
,则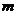 、
、 的大小关系为
.
的大小关系为
.
[解析]考查指数函数的单调性。 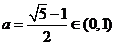 ,函数
,函数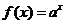 在R上递减。由
在R上递减。由 得:m<n
得:m<n
4.(2009北京理)若函数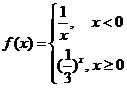 则不等式
则不等式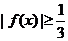 的解集为____________.
的解集为____________.
[答案]
[解析]本题主要考查分段函数和简单绝对值不等式的解法. 属于基础知识、基本运算的考查.
(1)由 .
.
(2)由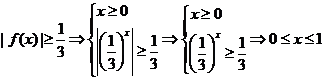 .
.
∴不等式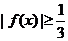 的解集为
的解集为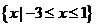 ,∴应填
,∴应填 .
.
3.(2009北京文)已知函数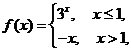 若
若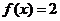 ,则
,则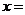 .
.
.w.w.k.s.5[答案]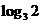
.w[解析]5.u.c本题主要考查分段函数和简单的已知函数值求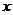 的值. 属于基础知识、基本运算的考查.
的值. 属于基础知识、基本运算的考查.
由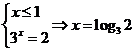 ,
,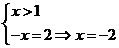 无解,故应填
无解,故应填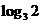 .
.
2.(2009上海卷文)
函数f(x)=x3+1的反函数f-1(x)=_____________.[答案]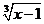
[解析]由y=x3+1,得x=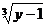 ,将y改成x,x改成y可得答案。
,将y改成x,x改成y可得答案。
1.(2009重庆卷理)若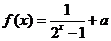 是奇函数,则
是奇函数,则 . [答案]
. [答案]
[解析]解法1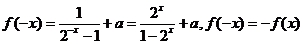
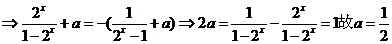
52.(2009福建卷文)若函数 的零点与
的零点与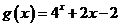 的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则 可以是
可以是
A. 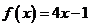 B.
B. 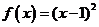 C.
C.  D.
D.
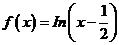
解析 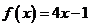 的零点为x=
的零点为x=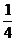 ,
,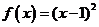 的零点为x=1,
的零点为x=1,  的零点为x=0,
的零点为x=0, 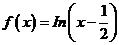 的零点为x=
的零点为x=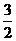 .现在我们来估算
.现在我们来估算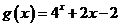 的零点,因为g(0)= -1,g(
的零点,因为g(0)= -1,g( )=1,所以g(x)的零点x
)=1,所以g(x)的零点x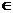 (0,
(0,
 ),又函数
),又函数 的零点与
的零点与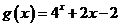 的零点之差的绝对值不超过0.25,只有
的零点之差的绝对值不超过0.25,只有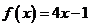 的零点适合,故选A。
的零点适合,故选A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com