
3.理解空间向量共线的充要条件理解共面向量定理
2.了解空间向量的概念、向量共面的含义,掌握空间向量的线性运算及其性质.
1.运用类比的方法,经历向量及其运算由平面向空间推广的过程.
3.1.1-3.1.2 空间向量及其线性运算、
共线向量定理和共面向量定理
[学习目标]
4.E,F,G,H分别为正方体ABCD-A1B1C1D1的棱A1B1,A1D1,B1C1,C1D1的中点.
求证:(1)E,F,D,B四点共面;
(2)平面AEF∥平面BDHG.
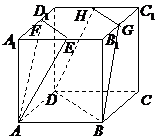
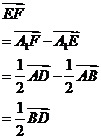

[问题反馈]
3.三棱锥O-ABC中,G,H分别是△ABC,
△OBC的重心,设
试用向量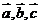 表示向量
表示向量

2.平行六面体ABCD-A’B’C’D’中,
求证: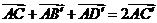
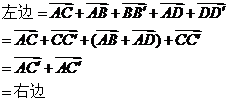
1.已知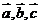 是不共面的三个向量,若它们的起点相同,且
是不共面的三个向量,若它们的起点相同,且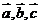 及
及 的终点共面,则实数t=_______
的终点共面,则实数t=_______
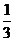
4.已知四棱锥P-ABCD的底面ABCD是平行四边形, E为PC的中点,(1)试用
E为PC的中点,(1)试用 表示向量
表示向量 ;
;
(2)证明:PA∥平面BED


题后小结
[巩固提高]
3.设 是两个不共线的向量,已知
是两个不共线的向量,已知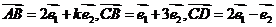 若A,B,D三点共线,求k的值.
若A,B,D三点共线,求k的值.
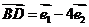

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com