
3、 补充例题 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=
补充例题 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=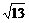 ,SB=
,SB=

(1)求证:SC⊥BC;
(2)求SC与AB所成角的余弦值
练习:
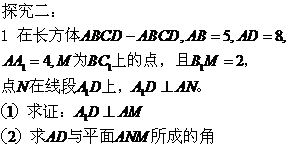

课 题:空间的角的计算(2)
预习目标:
能用向量方法解决二面角的计算问题
预习重点:二面角的计算
预习难点:二面角的计算
预习过程
2、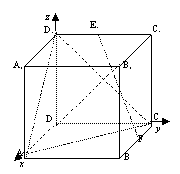 例2 在正方体
例2 在正方体 中, F分别是BC的中点,点E在D1C1上,且
中, F分别是BC的中点,点E在D1C1上,且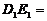
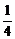 D1C1,试求直线E1F与平面D1AC所成角的大小
D1C1,试求直线E1F与平面D1AC所成角的大小
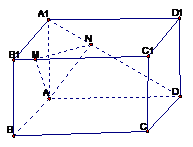
1、例1 在正方体 中,E1,F1分别在A1B1,,C1D1上,且E1B1=
中,E1,F1分别在A1B1,,C1D1上,且E1B1=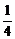 A1B1,D1F1=
A1B1,D1F1=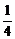 D1C1,求BE1与DF1所成的角的大小。
D1C1,求BE1与DF1所成的角的大小。
解1:
解2:
解3:
探究一:
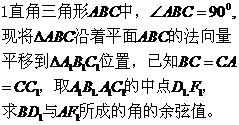

2、数量积
(1)设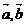 是空间两个非零向量,我们把数量
是空间两个非零向量,我们把数量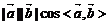 叫作向量
叫作向量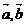 的数量积,记作
的数量积,记作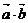 ,即
,即
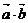 =
=
(2)向量的夹角:

(2)若 ,
, ,则
,则 .
.
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。
2、法向量在求线面角中的应用:
原理:设平面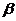 的斜线l与平面
的斜线l与平面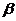 所的角为
所的角为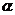 1,斜线l与平面
1,斜线l与平面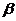 的法向量所成角
的法向量所成角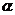 2,则
2,则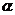 1与
1与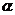 2
或与
2
或与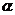 2的补角 。
2的补角 。
课前准备:
1、法向量在求面面角中的应用:
原理:一个二面角的平面角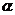 1与这个二面角的两个半平面的法向量所成的角
1与这个二面角的两个半平面的法向量所成的角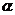 2 。
2 。
2、向量的夹角公式
1、异面直线所称的角、线面角的定义及求解方法
向量法求距离
3、例3(2005福建卷理第20题)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
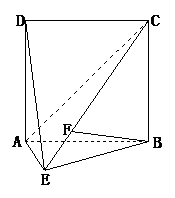 (Ⅰ)求证:AE⊥平面BCE;
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离。

解(Ⅰ)略
(Ⅱ)以线段AB的中点为原点O,OE所在直线为x轴,
AB所在直线为y轴,过O点平行于AD的直线为z轴,
建立空间直角坐标系O-xyz,如图.
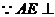 面BCE,BE
面BCE,BE 面BCE,
面BCE, 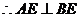 ,
,
在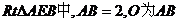 的中点,
的中点,
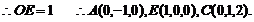
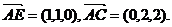 设平面AEC的一个法向量为
设平面AEC的一个法向量为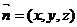 ,
,
则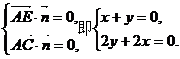 解得
解得
令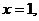 得
得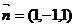 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为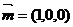 ,
,
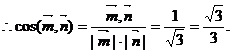
∴二面角B-AC-E的大小为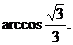
(III)略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com