
1.胶体的本质特征:分散质微粒直径在 之间。
3.考查对溶解度概念的理解。
教与学方案
[自学反馈]
2.运用胶体的性质解释生活中的实际问题。
1.从胶体与其它分散系的本质差异出发,考查鉴别胶体与溶液的常用方法。
21.(本小题满分12分)
(文)已知函数f(x)=()x,x∈[-1,1],函数g(x)=f2(x)-2af(x)+3的最小值为h(a).
(1)求h(a)的解析式;
(2)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.
19.(本小题满分12分)
(文)设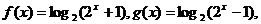 若关于
若关于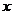 的函数
的函数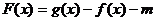 在
在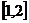 上有零点,求
上有零点,求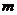 的取值范围。
的取值范围。
18. (本小题满分13分)某公司用480万元购得某种产品的生产技术后,再次投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为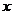 (元),年销售量为
(元),年销售量为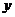 (万件),年获利为
(万件),年获利为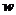 (万元).
(万元).
(1)请写出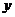 与
与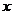 之间的函数关系式;
之间的函数关系式;
(2)求第一年的年获利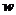 与
与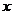 之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
17.(本小题满分13分)
设 为等比数列,且其满足:
为等比数列,且其满足: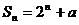 .
.
(1)求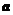 的值及数列
的值及数列 的通项公式;
的通项公式;
(2)已知数列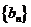 满足
满足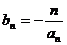 ,求数列
,求数列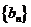 的前n项和
的前n项和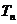 .
.
16.(本小题满分13分)
已知p: 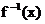 是
是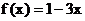 的反函数, 且
的反函数, 且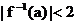 ;q : 集合
;q : 集合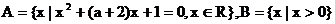 且
且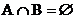 .求实数
.求实数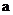 的取值范围, 使p或q为真,P且q为假。
的取值范围, 使p或q为真,P且q为假。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com