
1. 为防控甲流在人群中的进一步传播,我国科研人员已经研制生产出预防甲流的疫苗,并开始在人群中使用,下列关于甲流病毒和甲流疫苗的说法正确的是: 
A. 甲流病毒结构简单,只含有DNA和蛋白质
B. 甲流病毒在空气中可大量繁殖
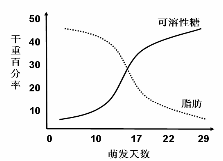 C. 为防止培养病毒的培养基被杂菌污染,需要用高温对培养基进行彻底的灭菌处理
C. 为防止培养病毒的培养基被杂菌污染,需要用高温对培养基进行彻底的灭菌处理
D. 接种过甲流疫苗的人同样有可能感染季节性流感
17.解:由已知,得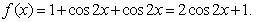 …………2分
…………2分
(1)最小正周期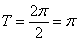 .
…………4分
.
…………4分
(2)令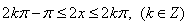 …………6分
…………6分
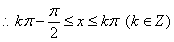 …………7分
…………7分
又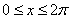 ,
,
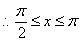 或
或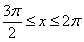 , …………9分
, …………9分
所以原函数的单调递增区间为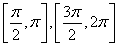 .
…………10分
.
…………10分
18解: 等差数列
等差数列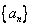 的前
的前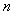 和为
和为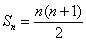
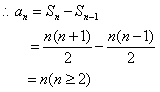 …………2分
…………2分
又当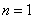 时,
时,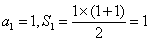 ,
,
 数列
数列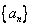 的通项公式为
的通项公式为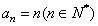 ………… 3分
………… 3分
由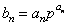 ,得
,得 .
.
所以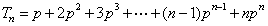 ,
…………4分
,
…………4分
当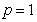 时,
时,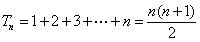 ;
…………5分
;
…………5分
当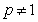 时,
时,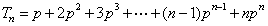
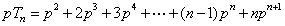 , …………7分
, …………7分
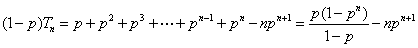 …9分
…9分
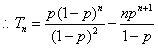 …………10分
…………10分
综上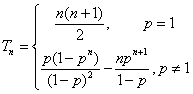 .
…………12分
.
…………12分
19解:(1)由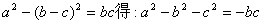 ………1分
………1分
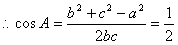 ………3分
………3分
又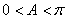
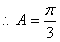 ………5分
………5分
(2)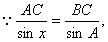
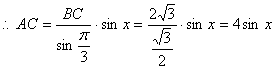 ………6分
………6分
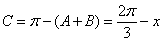 ,
,
同理: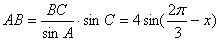 ………7分
………7分
 ………9分
………9分

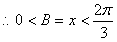 ………10分
………10分
故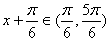 ,
,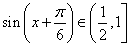 ,
,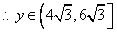 . ………12分
. ………12分
20解:(1)由题得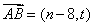 .
.

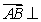
 ,
,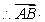

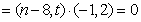 ,
……….2分
,
……….2分
得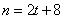 ,则
,则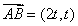 .
.
又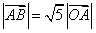 ,
,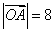 .
.
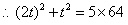 ,解得
,解得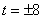 .
………4分
.
………4分
当 时,
时,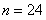 ;当
;当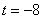 时,
时,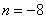 .
.
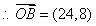 或
或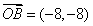 .
………6分
.
………6分
(2)由已知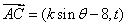
 向量
向量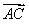 与向量
与向量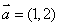 共线,
共线,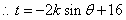 , ………7分
, ………7分
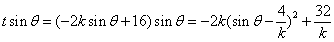 .
.
 ,
………8分
,
………8分
故当 时,
时, 取最大值
取最大值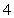 时,有
时,有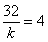 ,得
,得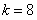 .
………10分
.
………10分
这时,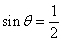 ,且
,且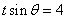 ,得
,得 ,则
,则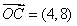 . ………11分
. ………11分
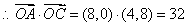 .
………12分
.
………12分
21解:(1)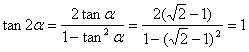 ………1 分
………1 分
又∵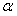 为锐角,∴
为锐角,∴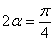 ………2分
………2分
∴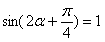
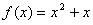 ………3分
………3分
(2)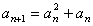 ∵
∵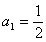 ∴
∴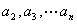 都大于0
都大于0
∴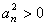 ∴
∴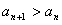 ………5分
………5分
(3) 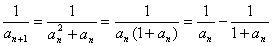
∴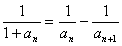 ………7分
………7分
∴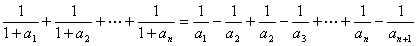
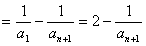 ………9分
………9分
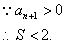 ………10分
………10分
∵ ,
, 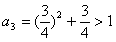 ,
,
又∵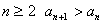 ∴
∴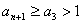 ∴
∴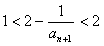
∴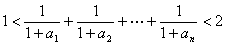 ………12分
………12分
22解:(1)由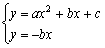 ,消去
,消去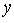 ,得
,得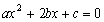 , ………1分
, ………1分
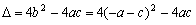
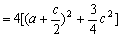 ………2分
………2分

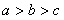 ,
,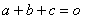
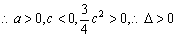 两函数的图象交于不同的两点
两函数的图象交于不同的两点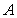 、
、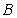 ………4分
………4分
(2)法一:
由已知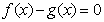 ,即为
,即为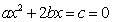 ………5分
………5分
由(1)知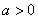 且上述方程一定有两不等实根
且上述方程一定有两不等实根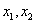
 ………6分
………6分
记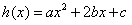 ,
,
则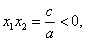
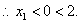 ………7分
………7分
又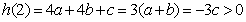
 ………8分
………8分
综上,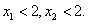
法二:
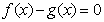 的两根为
的两根为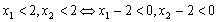
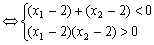 而
而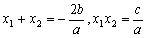
于是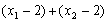
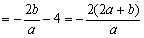
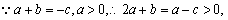
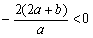
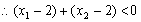 ,
,
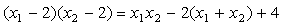
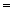
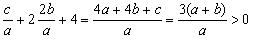
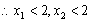
(3)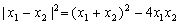
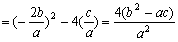
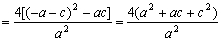
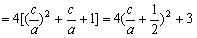 ………9分
………9分
由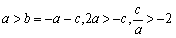 由
由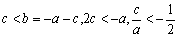 ………10分
………10分
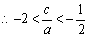 ,则
,则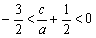 故
故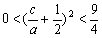
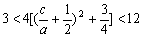 ,
,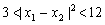 ………11分
………11分
又 ,故
,故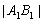 的取值范围为
的取值范围为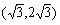 ………12分
………12分
13.9
14.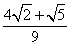 15.4018 16.① ③ ⑤
15.4018 16.① ③ ⑤
1.C 2.D 3.D 4.A 5.B 6.D 7.B 8.D 9.C 10.B 11.C 12.A
22.(本题满分12分)已知二次函数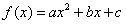 和一次函数
和一次函数 ,其中
,其中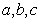 满足
满足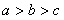 ,
,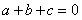 .
.
(1)求证:两函数的图象交于不同的两点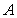 、
、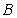 ;
;
(2)求证:方程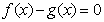 的两根都小于2;
的两根都小于2;
(3)求线段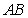 在
在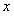 轴上射影
轴上射影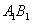 的长的取值范围.
的长的取值范围.













21.(本题满分12分)已知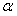 为锐角,且
为锐角,且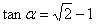 ,
,
函数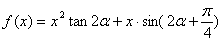 ,数列
,数列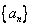 的首项
的首项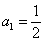 ,
, .
.
(1)求函数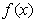 的表达式;
的表达式; 
(2)求证: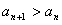 ;
;
(3)求证: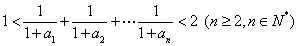 .
.

20.(本题满分12分) 在平面直角坐标系中,已知向量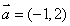 ,又点
,又点 ,
,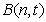 ,
,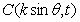
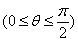 .
.
(1)若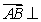
 ,且
,且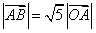
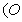 为坐标原点
为坐标原点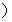 ,求向量
,求向量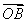 ;
;
(2)若向量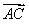 与向量
与向量 共线,当
共线,当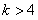 ,且
,且 取最大值
取最大值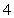 时,求
时,求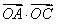 .
.

19.(本题满分12分)在△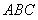 中,
中,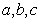 分别为角
分别为角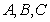 所对的边,且
所对的边,且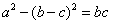 ,
,
(1)求角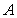 ;
; 
(2)若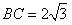 ,角
,角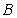 等于
等于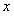 ,周长为
,周长为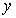 ,求函数
,求函数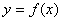 的取值范围
的取值范围

18.(本题满分12分)已知等差数列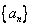 的前
的前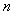 和为
和为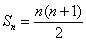 .记
.记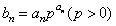 ,求数列
,求数列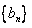 的前
的前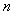 项和
项和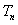 .
.

17.(本题满分10分)已知函数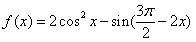 .
.
求:(1)函数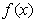 的最小正周期;
的最小正周期;
(2)函数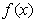 ,
,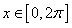 的单调增区间.
的单调增区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com