4.线圈在匀强磁场中转动产生交变电动势e=10sin20πt V，则下列说法正确的是 …(　　 )

A.t=0时，线圈平面位于中性面

B.t=0时，穿过线圈的磁通量为最大

C.t=0时，导线切割磁感线的有效速率最大

D.t=0.4 s时，e有最大值10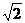V

答案：AB

3.如图5-1-8(a)所示，一矩形闭合线圈在匀强磁场中绕垂直于磁场方向的转轴OO′以恒定的角速度ω转动，当线圈平面与磁场方向平行时开始计时，线圈中产生的交变电流按照图(b)所示的余弦规律变化.在t=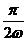时刻…(　　 )

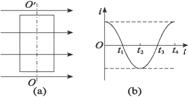
图5-1-8

A.线圈中的电流最大　　　　　　　　　　　 B.穿过线圈的磁通量为零

C.线圈所受的安培力为零　　　　　　　　　 D.线圈消耗的电功率为零

答案：CD

2.对于如图5-1-7所示的电流i随时间t做周期性变化的图象，下列描述哪些是正确的(　　 )

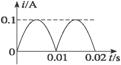
图5-1-7

A.电流的大小变化，方向也变化，是交流电

B.电流的大小变化，方向不变，不是交流电

C.电流的大小不变，方向不变，是直流电

D.以上说法都不正确

答案：B

1.一矩形线圈，绕垂直于匀强磁场并位于线圈平面内的固定轴转动，线圈中的感应电动势e随时间t的变化如图5-1-6所示.下列说法中正确的是(　　 )

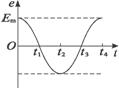
图5-1-6

A.t₁时刻通过线圈的磁通量为零

B.t₂时刻通过线圈的磁通量的绝对值最大

C.t₃时刻通过线圈的磁通量变化率的绝对值最大

D.每当e变换方向时，通过线圈的磁通量绝对值都为最大

答案：D

3.几种不同类型的交变电流

正弦式电流是一种最简单又最基本的交变电流，在电子电路中应用的交变电流，不只限于正弦式电流，它们随时间变化的规律是各式各样的，如图所示518。

图5-1-8

方法点拨　 方向随时间变化是交流电的最主要特征，也是交变电流和直流电的根本区别。

问题·思路·探究

问题1 交变电流是周期性变化的，由于线圈在磁场中匀速转动产生的电流应该是大小不变，方向时刻发生改变的，为什么电流随时间的变化呈正余弦规律呢？

思路：交变电流是由于线圈在磁场中匀速转动而产生的，虽然线圈是匀速转动的，但线圈切割磁感线的两条边并不是匀速转动的，由几何关系可以证明，也可将交变电接到示波器中进行观察。

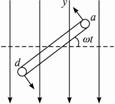
图5-1-9

探究：如图519所示，当线圈abcd经过中性面时开始计时，经时间t线圈转动的角度为ωt，ab、cd两边切割磁感线的有效速度为vsinωt。设线圈的长ab=l₁，宽ad=l₂，则v=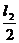ω，ab、cd边切割磁感线产生的电动势相同，均为Bl₁vsinωt，总电动势为e=Bl₁l₂ωsinωt，若线圈有n匝，则e=nBl₁l₂ωsinωt。所以产生的交变电流是呈正余弦规律。

问题2 线圈在磁场中匀速转动产生正弦交变电流，当线圈转至中性面时和磁场方向垂直，此时穿过线圈的磁通量最大，则电动势也应该为最大，为什么却是最小呢？

思路：线圈转至中性面时和磁场方向垂直，此时穿过线圈的磁通量虽然最大，但磁通量的变化率却最小为零，产生的电动势与磁通量的大小无关，仅与磁通量的变化率有关。

探究：电动势的大小与磁通量的大小无关，只与磁通量的变化率有关，可将发电机模型和电流表形成闭合回路，通过实验探究线圈在磁场中转动过程中电流的大小变化与线圈的位置关系。

典题·热题·新题

例1　 (2006江苏连云港高三调研)一矩形线圈绕垂直于匀强磁场方向、并位于线圈平面内的固定轴转动，线圈中的感应电动势e随时间t的变化情况如图5-1-10所示，则(　)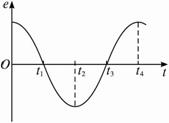

图5-1-10

A.t₁时刻穿过线圈的磁通量为零

B.t₂时刻穿过线圈的磁通量最大

C.t₃时刻穿过线圈的磁通量变化率为零

D.t₄时刻穿过线圈的磁通量为零

思路解析：本题主要考查交变电流的图象描述。由图象可知t₁和t₃时刻电动势为零，磁通量的变化率最小，线圈平面通常处于中性面位置，穿过线圈的磁通量最大，所以A错，C正确；t₂和t₄时刻电动势最大，磁通量的变化率最大，线圈平面通处于垂直中性面位置，穿过线圈的磁通量为零，所以B错，D正确。

答案：CD

方法归纳　 将交变电流的图象和交变电流的产生过程结合在一起综合进行考虑是处理此类问题的有效手段。由et图象知，当线圈处于中性面时，穿过线圈的磁通量最大，但变化率最小，产生的感应电动势为零。也可将et图象转化为Φt图象进行分析。

例2有一10匝正方形线框，边长为20 cm，线框总电阻为1 Ω，线框绕OO′轴以10π rad/s的角速度匀速转动，如图5-1-11，垂直于线框平面向里的匀强磁场的磁感应强度为0.5 T。问：

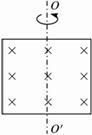
图5-1-11

(1)该线框产生的交变电流电动势最大值、电流最大值分别是多少？

(2)线框从图示位置转过60°时，感应电动势的瞬时值是多大？

(3)写出感应电动势随时间变化的表达式。

思路解析：本题主要考查交流电流的最大值及瞬时值的表达式。由瞬时值的表达式可直接求解。

解：(1)交变电流电动势最大值为E_m=2nBlv=2nBlωl/2=nBSω=10×0.5×0.2²×10×3.14 V=6.28 V,电流的最大值为I_m=E_m/R=6.28/1 A=6.28 A。

(2)线框转过60°时，感应电动势E=E_msin60°≈5.44 V。

(3)由于线框转动是从中性面开始计时的，所以瞬时表达式为

e=E_msinωt=6.28sin10πt(V).

方法点拨　 理解交变电流电动势瞬时值表达式的推导过程和推导中得到的结论是解决本题的关键。

例3 交流发电机产生的交流电动势为e＝E_msinωt(V)。如果将转子的转速提高一倍，匝数减少一半，其他条件保持不变，则交流电动势的表达式变为(　)

A.e＝2E_msinωt　　　　　

B.e＝E_msin2ωt

C.e＝E_msinωt

D.e＝2E_msin2ωt

思路解析：本题主要考查瞬时值与最大值之间的关系，由于瞬时值是由最大值及正弦函数值两部分决定的，只要找到条件变化后的最大值和角速度，问题即可解决。

因为ω＝2πn，当线圈的转速n加倍时，角速度ω也加倍。

根据电动势最大值的表达式E_m＝nBSω，可得E_m′＝E_m。

又ω′＝2ω，所以sinω′t＝sin2ωt，则产生的电动势为e′＝E_msin2ωt。

答案：B

误区警示　 交流发电机产生的交流电动势的瞬时值为e＝nBSω·sinωt，由公式确定影响最大值的因素是匝数、磁感应强度、线圈面积、角速度，而角速度同时又影响正弦函数值，可见公式的掌握是解决本题的关键。

例4 如图5-1-12甲所示，金属导轨水平放置，导轨上跨接一根金属棒ab，与导轨构成闭合回路并能沿导轨自由滑动。在导轨左侧与ab平行放置的导线cd中通以图5-1-12乙所示的交流电流，规定电流方向自c向d为正，则ab受到向左的安培力的作用时间是(　)

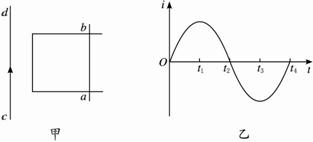
图5-1-12

A.0→t₁?

B.t₁→t₂?

C.t₂→t₃?

　D.t₃→t₄?

思路解析：在0→t₁时间内，i由c→d，由安培定则知，闭合回路中的磁场方向垂直纸面向里。因i增大，由楞次定律判断出闭合回路中有逆时针方向的感应电流，金属棒上电流为a→b，由左手定则可知，金属棒受到的安培力向左；在t₁→t₂时间内，i方向不变，逐渐减小，根据楞次定律知，闭合电路中有顺时针方向感应电流，由左手定则可知金属棒受到的安培力向右；在t₂→t₃时间内，金属棒受到的安培力向左，t₃→t₄时间内，金属棒受到的安培力向右；故选项A、C正确。

答案：AC

拓展延伸　 在导线中通入正弦交变电流，会产生变化的磁场，线框处于变化的磁场中会产生感应电流，线框总是以某种运动的趋势来阻碍其磁通量的变化。如在0→t₁时间段内电流为正且变大，通过线圈的磁通量要增大，而线框要阻碍其磁通量的增大，应向右运动，当然受到的安培力向右，又如t₃→t₄时间段内电流为负且变小，通过线框的磁通量要减小，而线框要阻碍其磁通量的减小，应向左运动，当然受到的安培力向左。

自我检测

基础达标

2.正弦交变电流的图象

从图5-1-5来分析，图(a)位置，线圈平面与中性面重合，此时无感应电流；经四分之一周期，线圈转动到图(b)位置，即最大值位置，感应电流达到最大，方向为abcda，规定该方向为正；再经过四分之一周期，线圈转动到图(c)位置，又到中性面，无感应电流；再经四分之一周期，线圈转动到图(d)位置，即最大值位置，感应电流又达到最大，但方向与先前相反，是adcba方向，负方向；再经四分之一周期，回到图(e)位置，经历了一个周期，电流又变为零，可见电流为零的位置是改变方向的位置。

上述变化可以用正弦图象(如图516)表达出来：

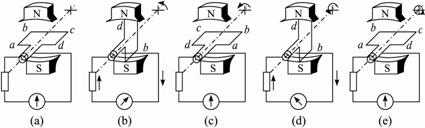
图5-1-5

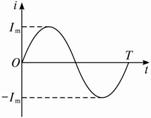
图5-1-6

电动势、电流、电压的变化规律如图5-1-7所示

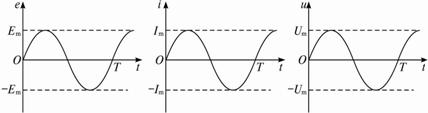
图5-1-7

1.交变电流的数学表达式

瞬时电动势：e=Emsinωt

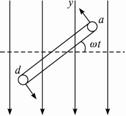
图5-1-4

瞬时电流：i=I_msinωt

瞬时电压：u=U_msinωt

在匀强磁场中，匀速转动的线圈里产生的感应电动势是按正弦规律变化的。

(1)规律推导：如图5-1-4所示，当线圈abcd经过中性面时开始计时，经时间t线圈转动的角度为ωt，ab、cd两边切割磁感线的有效速度为vsinωt。设线圈的长ab=l₁，宽ad=l₂，则v=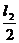，ab、cd边切割磁感线产生的电动势相同，均为?Bl₁vsinωt，两个电动势串联，总电动势为e=2Bl₁vsinωt。输出的电压瞬时值方程：u=U_msinωt

电流的瞬时值方程：i=I_msinωt

电动势按正弦规律变化，因此这种交变电流叫做正弦交流电。若从最大值位置计时，可以推导出电动势的余弦表达式。不管是正弦表达式还是余弦表达式我们都把它叫正弦交流电。

要点提示　 E是电动势的瞬时值，随着时间的变化而变化，不同时刻有不同的数值。E_max=2Blv为最大值，也叫电动势的峰值。上式表示形式仅限于自中性面开始计时的情况。当从垂直于中性面时，表达式应为e=E_mcosωt。

(2)交变电动势的最大值E_max=2Blv，当线圈abcd绕中心轴线(ad、bc中点连线)匀速转动时，设角速度为ω，则v=l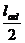ω，线圈的面积S=l_ad×l_bc，所以E_m=BSω,如果线圈匝数为n，则E _m=nBSω，由此可以看出，交变电动势的最大值由线圈的匝数n、磁感应强度B、转动角速度ω和线圈面积S决定，与线圈的形状无关，与转轴的位置无关。

产生正弦交流电的条件：匀强磁场、转轴与磁场垂直，线圈匀速转动，与转轴位置和线圈形状无关。

2.中性面

线圈平面与磁感线垂直的位置叫中性面。

疑点突破　 感应电动势跟磁通量大小无关，而跟磁通量的变化率成正比，所以，当线圈转至中性面时，虽然磁通量最大，但磁通量的变化率却最小，等于零(导体不切割磁感线)，因此当线圈处于中性面时，感应电动势为零，感应电流为零，恰好是电流改变方向的位置。由于线圈转一周有两次经过中性面，所以每转一周电流方向改变两次。线圈垂直中性面时，虽然磁通量等于零，但是磁通量的变化率却最大，因此感应电动势最大，感应电流最大。

1.交变电流产生的实验探究

如图5-1-1所示，利用手摇式发电机模型探究交变电流的产生过程。手摇式发电机和灯泡电流计连接构成闭合回路。发电机的原理：线圈abcd处在磁场中，线圈的ab边和cd边连在金属滑环上；用导体做的两个电刷分别压在两个滑环上，线圈在转动时可以通过滑环和电刷保持与外电路连接，如图5-1-2。

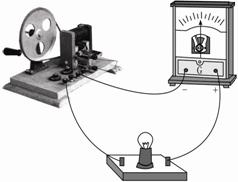
图5-1-1

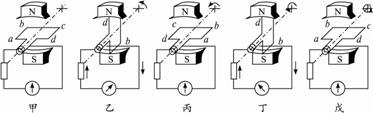
图5-1-2

结合线圈在磁场中转动截面图5-1-3，判断如下：

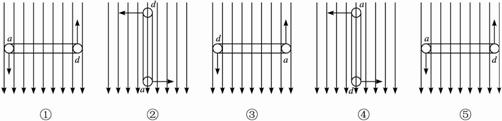
图5-1-3

甲：线圈中没有电流　　乙：电流从a流向b　　丙：线圈中没有电流

丁：电流从b流向a　　戊：线圈中没有电流

实验结论：线圈每转一周，电流方向改变两次，电流改变方向的时刻也就是线圈中无电流的时刻(或者说磁通量最大的时刻)。

由于线圈转一周的过程中，线圈的磁通量有两次达到最大，故电流的方向在线圈转一周的过程中改变两次。

4.电流的分类：按大小和方向的变化规律，可将电流作如下的分类：

方向随时间做周期性变化是交流电的最重要特征。恒定电流仅仅是直流中的一种；同样，交变电流也并不都是正弦交变电流，正弦交变电流的特殊规律不能适用所有交流电。