
4.已知在四边形ABCD中,有 ·
·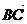 =
=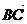 ·
· =0,则该四边形是
=0,则该四边形是
A.平行四边形 B.矩形
C.直角梯形 D.矩形或直角梯形
3.对于任意k∈[-1,1],函数f(x)=x2+(k-4)x-2k+4的值恒大于零,则x的取值范 围是
A.x<0 B.x>4
C.x<1或x>3 D.x<1
2.函数f(x)=2-x+1的反函数图象大致是

1.若X={x|x=4n+1,n∈Z},Y={y|y=4n-3,n∈Z|,Q={z|z=8n+1,n∈Z},则X、Y、Q的关系是
A.Q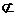 Y
Y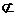 X B.X
X B.X Y
Y Q
Q
C.Q X=Y D.X=Y=Q
X=Y D.X=Y=Q
22.解:(1)∵ ∴
∴  ………2分
………2分
当 时,
时,
 ,
,
∴  ,
,
∴
 ……………5分
……………5分
当 时,
时, 也满足上式,
也满足上式,
∴数列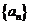 的通项公式为
的通项公式为 …6分
…6分
(2)
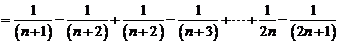
 ………………………8分
………………………8分
令 ,则
,则 ,
当
,
当 恒成立
恒成立
∴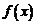 在
在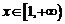 上是增函数,故当
上是增函数,故当 时,
时,
即当 时,
时,  ……………………11分
……………………11分
另解: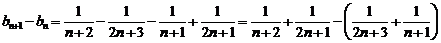

∴数列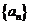 是单调递减数列,∴
是单调递减数列,∴
20.(1)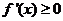 恒成立
恒成立
(2)
(3)
21 解(1)当 时,
时,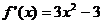
令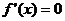 得
得 .
.
所以 在
在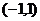 上单调递减,在
上单调递减,在 和
和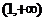 上单调递增.
上单调递增.
所以 的极小值为
的极小值为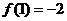
(2)因为 在
在 上为偶函数,故只求在
上为偶函数,故只求在 上的最大值即可.
上的最大值即可.
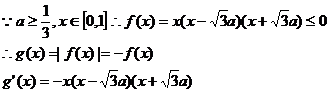
当 时,
时, ,
, 在
在 上单调递增,
上单调递增,
当 时,
时, 在
在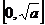 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
所以可得
19.(1)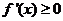 恒成立
恒成立
(2) (3)
(3)
18.由 1
1
得 2
2
1-2得: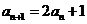

所以
故数列 是从第2项开始的等比数列.
是从第2项开始的等比数列.

所以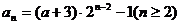
而 不满足上式
不满足上式
所以

(2)由 ,
, ,则
,则
使用错位相减法可得: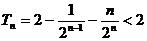
22.已知数列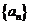 中,
中, .
.
(1)写出 的值(只写结果)并求出数列
的值(只写结果)并求出数列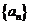 的通项公式;
的通项公式;
(2)设 ,若对任意的正整数
,若对任意的正整数 ,当
,当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。

21. 已知函数
(1)当 时,求
时,求 的极小值;
的极小值;
(2)设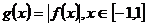 ,求
,求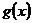 的最大值
的最大值 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com