6．不等式对任意恒成立，则实数的取值范围为

A．　 B．　　　 　

C．　　 D．

5．有下列四个命题：　 ①“若, 则互为相反数”的逆命题；　 ②“全等三角形的面积相等”的否命题；　 ③“若，则有实根”的逆否命题； ④“不等边三角形的三个内角相等”逆命题；其中真命题为

A．①②　　 　　 B．②③　　　　　 　　 C．③④　　　　　 D．①③

4．函数的一个单调递减区间是

A．　　 　　　　 B．　　 　 C．　　 　　　 D．

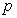3．已知, 则是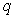的(　　　 )条件.

　 　A．充要　　　 　B．充分不必要 　　　C．必要不充分　 　D．既不充分也不必要

2．若复数(∈R，为虚数单位位)是纯虚数，则实数的值为

A．　 　　 　　B．6　 　　　 　　C．4　　　 　　　 　D．-2

1．设A、B是非空集合，定义，已知，，则等于

A．　 　 B．　　 C．　　 D．

22．

解：(1)∵

　 ∴………………1分

　 ∵ 当　

∴………………………3分

有两个不相等的实根

∴存在极值

∴存在极值时，a的取值范围是：………………4分

(2)∵

∴对任意恒成立………5分

∵，∴的对称轴………6分

　若, 时，则

∴对任意恒成立，∴………8分

若为单减函数

∴

∴ ∴　 ………11分

可知：

上为增函数时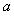，的取值范围是………12分

21．

解:(1) ∵>0且2－x≠0 ∴的定义域为 ………………1分

判断在上是增函数，下证明之：………………2分

设任………………3分

∵

∴………………4分

∵ ∴x₂－x₁＞0，2－x₁＞0，2－x₂＞0，

则………………5分

∵

∴且

又∵

∴

∴ ∴………………6分

∴，则………………7分

∴根据增函数的定义可知：在上是增函数. ………………8分

(2)证明: ∵，_，∴………………9分_，

∴是的一个根._，，，………………10分

∵在上是增函数　 ∴在其定义域上也为增函数………………11分

∴不可能还有一个解，不然这与在其定义域上为增函数相矛盾

故有唯一解. ………………12分

19．

解：(1)简单随机抽样是等可能抽样，甲、乙、丙三人被抽查的概率均为…………3分，

故他们中恰有2人被抽查的概率为…………6分

(2)简单随机抽样是等可能抽样，故每组为最佳抽查的概率为　 ……9分

每组为最佳抽查的概率相同，抽查5组可以看成做5次独立重复试验，故全班5组中恰

22．(本小题满分12分)

已知函数其中，

(1)若在时存在极值，求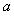的取值范围；

(2)若在上是增函数，求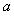的取值范围.