
例1.A、B两小球在光滑水平面上沿同一直线同方向运动共动量分别为PA=5kgm/s,PB=7kgm/s,若A追上B后与B碰撞,碰后B的动量为PB/ =10kgm/s,则A、B的质量之比可能为
A.1 :1 B.1 :2 C.1 :5 D.1 :10
分析:此例的求解除了运用碰撞的规律外,还需要关注到碰撞的特征与制约碰撞过程的相关因素。
解答:由“动量制约”知:碰撞过程中A、B两球的总动量应守恒即:
PA+PB=PA/+PB/
由此得:碰后A球动量为
PA/=PA+PB-PB/=2kgm/s
由“动能制约”知:碰前总动能不小于碰后总动能,即
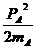 +
+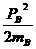 ≥
≥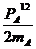 +
+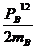
代入数据有
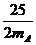 +
+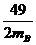 ≥
≥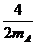 +
+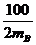
于是可得
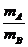 ≤
≤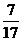
由“运动制约”知:考虑到碰后运动的合理性,碰后A球的速度应不大于B球的速度,即
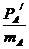 ≤
≤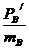
代入数据又有
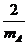 ≤
≤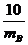
于是又可得
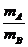 ≥
≥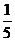
由此知:此例应选C。
例2.试将上述“人船模型”的四种变例给出定量解答。
分析:确认了四种变例其物理本质与“人船模型”相同,于是例可以直接运用相应的结论。
解答:(1)变例1中的“人车模型”与“人船模型”本质相同,于是直接得
S2=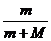 L
L
解答:(2)变例2中的h实际上是人相对于地的位移S1,而绳长则是人与气球的相对位移L,于是由
h=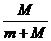 L
L
可解得:绳长至少为
L=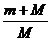 h
h
解答(3):变例3中小球做的是复杂的曲线运动,但只考虑其水平分运动,其模型例与“人船模型”相同,而此时的相对位移大小为2R,于是物体M沿水平而向右移动的最大距离为
S2=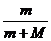 ·2R
·2R
解答(4):变例4中环的质量取得某种极端的值
m→0
 于是所求的小球沿水平方向移动的距离应为
于是所求的小球沿水平方向移动的距离应为
S2=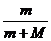 L→0
L→0
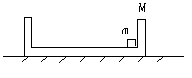
 例3.如图7所示,质量M=2kg的盒子放在
例3.如图7所示,质量M=2kg的盒子放在
光滑的水平面上,盒子长L=1m,质量为m=1kg的小物
块从盒子的右端以υ0=6m/s的初速度向左运动,小物
块与盒子底部间动摩擦因数μ=0.5,与盒子两侧壁间的碰撞无机械能损失,则小物块最终将相对静止于盒子的何处?
分析:一方面小物块和盒子间相对运动和相互碰撞过程中要遵从动量守恒定律,另一方面小物块和盒子间相对运动时滑动摩擦将使系统的动能减少,于是有
解答:由动量守恒定律得
mυ0=(m+M)υ
由公式“fd=△EK”又可得
μmgd= mυ02-
mυ02- (m+M)υ2
(m+M)υ2
代入数据可解得:从开始运动到小物块与盒子相对静止的过程中,小物块的相对路程为
d=2.4m
由此知:小物块最终相对静止于距盒子右端0.4m处.
3. “fd=△EK”的运用
“fd=△EK”的运用
(1)公式“fd=△EK”的含意.
如图6所示,:质量M的木块放在光滑水
平面上,质量为m的子弹以水平速度υ0射入木块,
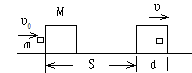 若射入的深度为d,后子弹与木块的共同速度为υ,
若射入的深度为d,后子弹与木块的共同速度为υ,
射入时子弹与木块间相互作用的力的大小为f,则:
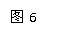 相互作用的力f与相时位移的大小d的乘积,恰等于
相互作用的力f与相时位移的大小d的乘积,恰等于
子弹与木块构成的系统的动能的减少量.即:
fd=△EK= mυ02-
mυ02- (m+M)υ2
(m+M)υ2
(2)公式“fd=△EK”的依据.
实际上公式“fd=△EK”是过立在动能定理的基础之上的:仍如图-6所示,对子弹和木块分别运用动能定理可得.
―f(s+d)= mυ2―
mυ2― mυ02
mυ02
fs= Mυ2
Mυ2
将此两代劳相加后整理即可得
fd= mυ02―
mυ02― (m+M)υ2=△EK.
(m+M)υ2=△EK.
(3)公式“fd=△EK”的运用
如果是两个物体构成的系统运动过程中除了相互作用的滑动摩擦力外,系统的外力为零,则都可以运用公式
fd=△EK
来制约系统运动中的能量的转多与转化,应该注意的是:当构成系统的双方相对运动出现往复的情况时,公式中的d就理解为“相对路程”而不应该是“相对位移的大小”。
2.“人船模型”的研究
(1)“人船模型”
 典型的力学过程通常是典型的模型所参与和经历的,而参与和经历力学过程的模型所具备的特征,将直接影响着力学过程的发生,发展和变化,在将直接影响着力学过程的分析思路,在下列力学问题中我们将面临着一个典型的“人船模型”。
典型的力学过程通常是典型的模型所参与和经历的,而参与和经历力学过程的模型所具备的特征,将直接影响着力学过程的发生,发展和变化,在将直接影响着力学过程的分析思路,在下列力学问题中我们将面临着一个典型的“人船模型”。
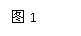 问题:如图 1所示,质量为M的小船长L,
问题:如图 1所示,质量为M的小船长L,
静止于水面,质量为M的小船长为L,静止于水面,
质量为m的人从船左端走到船右端,不计水对船的
运动阻力,则这过程中船将移动多远?
(2)“人船模型”的力学特征
如能关注到如下几点就可以说基本上把握住了“
人船模型”的力学特征了:“人船模型”是由人和船两个物体构成的系统;该系统在人和船相互作用下各自运动,运动过程中该系统所受到的合外力为零;而系统的合外力为零则保证了系统在运动过程中总动量守恒。
(3)“人船模型”的分析思路。
①分析“人船模型”运动过程中的受力特征,进而判断其动量守恒,得
mυ=Mu
②由于运动过程中任一时刻人,船速度大小υ和u均满足上述关系,所以运动过程中,人、船平均速度大小,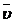 和
和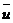 也应满足相似的关系。即
也应满足相似的关系。即
m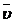 =M
=M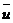
③在上式两端同乘以时间,就可得到人,船相对于地面移动的距离S1和S2的关系为
mS1=MS2
④考虑到人、船相对运动通过的距离为L,于是得
S1+S2=L
⑤由此即可解得人、船相对于地面移动的距离分别为
 S1=
S1=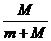 L
L
S2=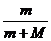 L
L
(4)“人船模型”的几种变例.
 ①把“人船模型”变为“人车模型”.
①把“人船模型”变为“人车模型”.
变例1:如图2所示,质量为M,长为L的
平板小车静止于光滑水平面上,质量为m的人从车左
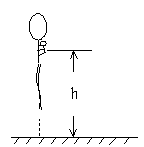 端走到车右端的过程中,车将后退多远?
端走到车右端的过程中,车将后退多远?
②把水平方向的问题变为竖直方向。
变例2:如图3所示,总质量为M的足球下
端悬着质量为m的人而静止于高度为h的空中,欲使
人能完全沿强着地,人下方的强至少应为多长?
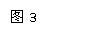 ③把直线运动问题变为曲线运动.
③把直线运动问题变为曲线运动.
变例3:如图4所示,质量为M的物体静止
于光滑水平面上,其上有一个半径为R的光滑半球
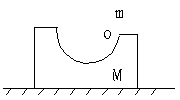 形凹面轨道,今把质量为m的小球自轨道右测与球
形凹面轨道,今把质量为m的小球自轨道右测与球
心等高处静止释放,求M向右运动的最大距离。
④把模型双方的质量比变为极端情况.
变例4:如图5所示,光滑水平杆上套有
 一个质量可忽略的小环,长L的强一端系在环上下,
一个质量可忽略的小环,长L的强一端系在环上下,
另一端连着质量为M的小球,今使小球与球等高且
将绳拉直,当把小球由静止释放直到小球与环在同
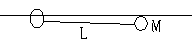 一竖直线上,试分析这一过程中小球沿水平方向的移动距离.
一竖直线上,试分析这一过程中小球沿水平方向的移动距离.
1.“碰撞过程”的分析
(1)“碰撞过程”的特征.
“碰撞过程”作为一个典型的力学过程其特征主要表现在如下两个方面:
第一,经历的时间极短,通常情况下,碰撞所经历的时间在整个力学过程中都是可以初忽略的;第二碰撞双方相互作用的内力往往是远大于来自外部物体的作用力
(2)“碰撞过程”的规律
正是因为“碰撞过程”所具备的“作用时间短”和“外力很小”(甚至外力为零)这两个特征,才使得碰撞双方构成的系统在碰撞前后的总动量遵从守恒定律,即
m1υ1+m2υ2=m1u1+m2u2
(3)“碰撞过程”的分类。
按照形变恢复情况划分:碰撞过程中所产生的形变能够完全恢复的称为弹性碰撞;碰撞过程中所产生的形变不能够完全恢复的称为非弹性碰撞;碰撞过程中所产生的形变完全不能够恢复的称为完全非弹性碰撞。
按照机械能损失的情况划分:碰撞过程中没有机械能损失的称为弹性碰掸撞;碰撞过程中有机械能损失的称为非弹性碰撞;碰撞过程中机械能损失最多的称为完全非弹性碰撞。
(4)“碰撞过程”的特例.
弹性碰撞作为碰撞过程的一个特例,它是所有碰撞过程的一种极端的情况:形变能够完全恢复;机械能丝毫没有损失。弹性碰撞除了遵从上述的动量守恒定律外,还具备:碰前、碰后系统的总动能相等的特征,即
 m1υ12+
m1υ12+ m2υ22=
m2υ22= m1u12+
m1u12+ m1u12
m1u12
由此即可把弹性碰撞碰后的速度u1和u2表为
u1=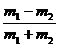 υ1+
υ1+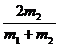 υ2
υ2
u2=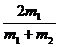 υ1+
υ1+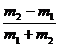 υ2
υ2
如对弹性碰撞的速度表达式进一步探讨,还会发现另一特征:弹性碰撞前,碰后,碰撞双方的相对速度大小相等,即
u2-u1=υ1-υ2
完全非弹性碰撞作为碰撞过程的一个特别,它是所有碰撞过程的另一种极端的情况:形变完全不能够恢复;机械能损失达到最大。正因为完全非弹性碰撞具备了“形变完全不能够恢复”。所以在遵从上述的动量守恒定律外,还具德:碰撞双方碰后的速度相等的特征,即
u1=u2
由此即可把完全非弹性碰撞后的速度u1和u2表为
u1=u2=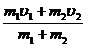
而完全非弹性碰撞过程中“机械能损失最大”的特征可以给出如下证明:碰撞过程中机械能损失表为
△E= m1υ12+
m1υ12+ m2υ22―
m2υ22― m1u12―
m1u12― m2u22
m2u22
由动量守恒的表达式中得
u2=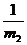 (m1υ1+m2υ2-m1u1)
(m1υ1+m2υ2-m1u1)
代入上式可将机械能的损失△E表为u1的函数为
△
E=-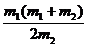 u12+
u12+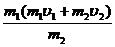 u1+[(
u1+[( m1υ12+
m1υ12+ m2υ22)
m2υ22)
-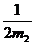 ( m1υ1+m2υ2-m1u1)2]
( m1υ1+m2υ2-m1u1)2]
这是一个二次项系数小于零的二次三项式,显然:当
u1=u2=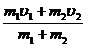
时,即当碰撞是完全非弹性碰撞时,系统机械能的损失达到最大值
△Em= m1υ12+
m1υ12+ m2υ22-
m2υ22-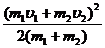
(5)“碰撞过程”的制约
通常有如下三种因素制约着“碰撞过程”。
①动量制约:即碰撞过程必须受到“动量守恒定律的制约”;
②动量制约:即能机械碰撞过程,碰撞双方的总动能不会增加;
③运动制约:即碰撞过程还将受到运动的合理性要求的制约,比如,某物体向右运动,被后面物体迫及而碰撞后,其运动速度只会增大而不应该减小。
(6)“碰撞过程”的推广。
相互作用的双方在相互作用过程中系统所受到的合外力为零时,我们可以将这样的过程视为“广义的碰撞过程”加以处理。
22. ㈠(本题满分7分)已知曲线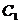 的参数方程为
的参数方程为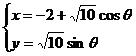 (
(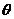 为参数),曲线
为参数),曲线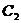 的极坐标方程为
的极坐标方程为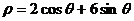 .
.
(1)将曲线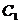 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线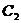 的极坐标方程化为直角坐标方程;(2)曲线
的极坐标方程化为直角坐标方程;(2)曲线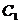 与
与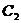 是否相交,请说明理由.
是否相交,请说明理由.
㈡ (本题满分7分)已知矩阵A=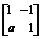 ,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).
,其中a∈R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3).
(1)求实数a的值;(2)求矩阵A的特征值及特征向量.
21. (本题满分12分)已知函数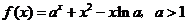 .
.
①求证: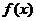 在
在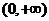 上单调递增;
上单调递增;
②函数 有三个零点,求
有三个零点,求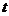 值;
值;
③对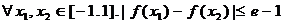 恒成立,求
恒成立,求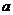 的取值范围。
的取值范围。
20. (本题满分12分)已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
19. (本题满分12分)在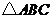 中,
中,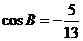 ,
,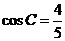 .
.
(Ⅰ)求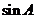 的值;
的值;
(Ⅱ)设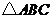 的面积
的面积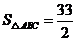 ,求
,求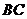 的长.
的长.
18.(本题满分12分)设集合 ,
,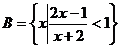 ,
,
若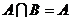 。求实数a的取值范围。
。求实数a的取值范围。
17.(本题满分12分) 设函数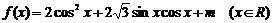 。
。
(Ⅰ)求函数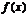 的最小正周期;
的最小正周期;
(Ⅱ)若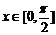 ,是否存在实数m,使函数
,是否存在实数m,使函数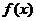 的值域恰为
的值域恰为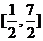 ?若存在,请求出m的取值;若不存在,请说明理由.
?若存在,请求出m的取值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com