
2、了解目前我国相关癌症的发病率和死亡率
1、分析癌症的病因和预防措施
21.解:解:(1)f ′(x)=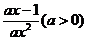 依题
依题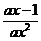 ≥0在[1,+∞)上恒成立
≥0在[1,+∞)上恒成立
即a≥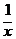 在[1,+∞)上恒成立,∴a≥1 ……
在[1,+∞)上恒成立,∴a≥1 ……
(2)当a=1时,f ′(x)=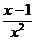 ,其中x∈[
,其中x∈[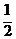 ,2], 而x∈[
,2], 而x∈[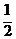 ,1)时,f ′(x)<0;x∈(1,
,1)时,f ′(x)<0;x∈(1,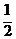 ]时,f ′(x)>0,
∴x=1是f (x)在[
]时,f ′(x)>0,
∴x=1是f (x)在[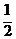 ,2]上唯一的极小值点,∴ [f (x)]min=f (1)=0 又f (
,2]上唯一的极小值点,∴ [f (x)]min=f (1)=0 又f (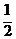 )-f (2)=
)-f (2)=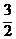 -2ln2=
-2ln2=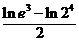 >0,∴f (
>0,∴f (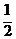 )>f (2),
∴[f (x)]max=f (
)>f (2),
∴[f (x)]max=f (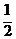 )=1-ln2
)=1-ln2
综上,a=1时,f (x)在[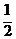 ,2]上的最大值和最小值分别为1-ln2和0
,2]上的最大值和最小值分别为1-ln2和0
(3)若a=1时,由(1)知f (x)=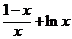 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,
当n>1时,令x=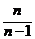 ,则x>1,故f (x)>f (1)=0,
,则x>1,故f (x)>f (1)=0,
即f (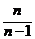 )=
)=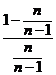 +ln
+ln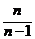 =-
=-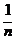 +ln
+ln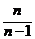 >0,∴ln
>0,∴ln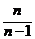 >
>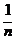
20. 解: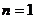 时,由
时,由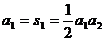 及
及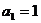 得
得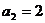
当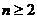 时,
时,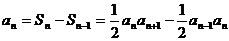 得
得
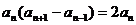
因为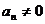 ,所以
,所以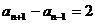
从而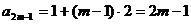
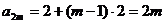

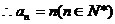
②由①知,不等式
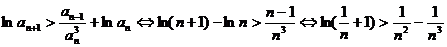
只需证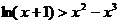 即
即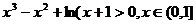
令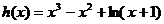
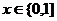
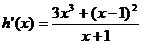 在
在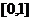 上恒正,所以
上恒正,所以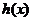 在
在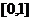 上单调递增,当
上单调递增,当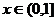 时,恒有
时,恒有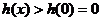 即原不等式得证
即原不等式得证
19. 解:(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡。设事件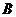 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件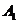 为“采访该团3人中,1人持金卡,0人持银卡”,事件
为“采访该团3人中,1人持金卡,0人持银卡”,事件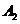 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。 
 .
.  ------------------------------------------------
------------------------------------------------
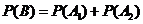
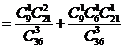
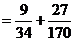
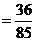 , 所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是
, 所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是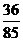 。-----------------------7分
。-----------------------7分
(Ⅱ)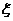 的可能取值为0,1,2,3 ,
的可能取值为0,1,2,3 ,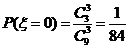 ,
, 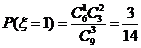 .
. 

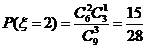 ,
,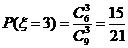 ,.
,.  ---------------------------- 10分
---------------------------- 10分
 所以
所以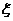 的分布列为
的分布列为
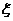 |
0 |
1 |
2 |
3 |
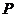 |
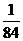 |
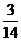 |
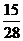 |
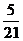 |
所以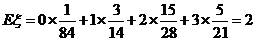 , ……………………12分
, ……………………12分
17、解:(1) 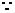 平面ABCD
平面ABCD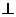 平面ABEF,
平面ABEF,
且四边形ABCD与ABEF是矩形,
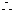 AD
AD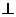 平面ABEF,
平面ABEF,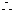 AD
AD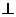 AE,
AE,
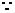 BC∥AD
BC∥AD 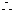 BC
BC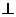 AE
AE
又FD=2,AD=1,所以AF=EF=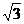 ,所以四边形ABEF为正方形.
,所以四边形ABEF为正方形.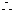 AE
AE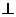 FB,
FB,
又BF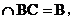 BF
BF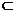 平面BCF,BC
平面BCF,BC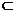 平面BCF
平面BCF
所以AE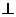 平面BCF……………………………………………4分
平面BCF……………………………………………4分
(2)设BF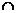 AE=O,取FD的中点为H,连接OH,在
AE=O,取FD的中点为H,连接OH,在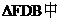 OH//BD,
OH//BD,
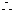
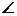 HOF即为异面直线BD与AE所成的角(或补角),
HOF即为异面直线BD与AE所成的角(或补角),
在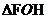 中,OH=1,FH=1,FO=
中,OH=1,FH=1,FO= ,
, cos
cos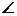 HOF=
HOF=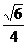
 异面直线BD与AE所成的角的余弦值为
异面直线BD与AE所成的角的余弦值为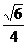 ………………………….8分
………………………….8分
(3)当N为FD的中点时, MN∥平面FCB
证明:取CD的中点G,连结NG,MG,MN,
则NG//FC,MG//BC, 又NG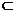 平面NGM,MG
平面NGM,MG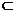 平面NGM且NG
平面NGM且NG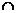 MG=G
MG=G
所以平面NGM//平面FBC,
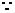 MN
MN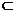 平面NGM
平面NGM
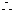 MN//平面FBC……………………………………………………………12分
MN//平面FBC……………………………………………………………12分
(18)解:
(Ⅰ)由题意,c=1,可设椭圆方程为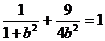 ,解得
,解得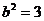 ,
,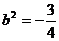 (舍去)
(舍去)
所以椭圆方程为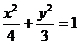 。
……………4分
。
……………4分
(Ⅱ)设直线AE方程为: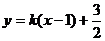 ,代入
,代入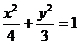 得
得
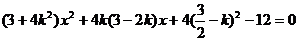
设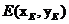 ,
,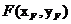 ,因为点
,因为点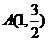 在椭圆上,所以
在椭圆上,所以
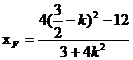
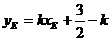 ………8分
………8分
又直线AF的斜率与AE的斜率互为相反数,在上式中以-K代K,可得
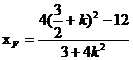

所以直线EF的斜率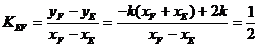
即直线EF的斜率为定值,其值为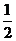 。
……13分
。
……13分
16.解:(1)
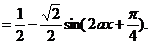 …………………………………(2分)
…………………………………(2分)
由题意可知: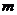 为函数
为函数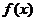 的最值,且
的最值,且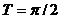 ,
, ,
,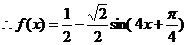 ,
,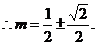 ………………………(6分)
………………………(6分)
(2)令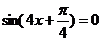 ,则
,则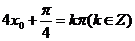 ,
,
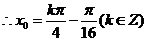 ,由
,由 ,
,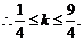
又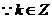 ,
,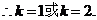
点A的坐标为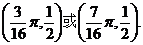 …………………………………(12分)
…………………………………(12分)
11. 360 12. 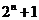 13. (1)(2) 14.
13. (1)(2) 14.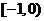 15.
15. 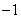 .
.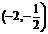 (注:第一空2分,第二空3分.)
(注:第一空2分,第二空3分.)
1-5CDACC 6-10 DCAB 10.答案:B,解析:由题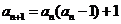 ,则
,则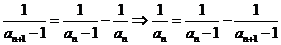 ,故有
,故有
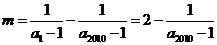 ,由于
,由于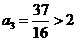 且
且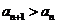 ,故
,故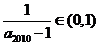 ,所以
,所以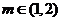 ,其整数部分是
,其整数部分是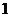 .
.
21. ( 13分)已知函数f (x)=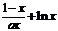 。(1)若函数f (x)在[1,+∞)上为增函数,求正实数
。(1)若函数f (x)在[1,+∞)上为增函数,求正实数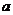 的取值范围;(2)当
的取值范围;(2)当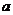 =1时,求f
(x)在[
=1时,求f
(x)在[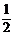 ,2]上的最大值和最小值。(3)求证:对于大于1的正整数n,
,2]上的最大值和最小值。(3)求证:对于大于1的正整数n,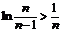 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com