7.小明家使用瓶装煤气，瓶的容积为 0.015 m³，冬季换气时够55元.暑假的一天小明发现煤气价格跌至51元／瓶，而刚刚报纸上报道油气价格上涨了，这是怎么回事呢？他查找了煤气资料：煤气冬季密度0.88×10³kg/m³，夏季0.8×10³ kg／m³.经过计算他终于明白了原因.试帮他计算和回答：

(1)冬季和夏季一瓶煤气的质量各多少千克？

(2)以质量计价，冬季煤气价格是多少元/千克？

(3)若油价未变，夏季煤气应为多少元／瓶？

(4)小明家暑假装的这次煤气到底是涨了还是跌了？

6.医院ICU重症监护室内配有充满氧气的钢瓶，供病人急救时使用，其密度为5 kg／m³.若某次抢救病人用去瓶内氧气一半，则瓶内剩余的氧气的质量将　　　　　　　　　 (选填“变大”／变小”或“不变”),其密度为　　　　　　　　　　　　 kg／m³.

5.如图2.3-7，某城市有座大理石雕像，已知其质量为18.5t，它的体积约为　　　　　　 m³(大理石的密度为2.6-2.8×10³kg/m³).

图2.3-7　 雕塑“思想者”

4.(2004·北京市)下列有关密度的说法，正确的是(　　 　)

A.一滴水的密度小于一桶水的密度

B.因为铝比铁轻，所以铝的密度小于铁的密度

C.液体的密度一定小于固体的密度

D.密度是物质的一种特性

3.有四个用同一物质制成的相似正方体，它们的棱长和质量如图2.3-6所示，其中有一个是空心的，它是(　　 )

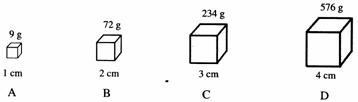
图2.3-6

2.(潍坊实验区中考题)金属锇的密度为22.6×10³kg/m³，中子星每1cm³的质量10³g.脉冲星核的密度为10¹⁵g/cm³，超巨星的密度是氢气密度的 17万分之一.上述物质密度最大的是( 　　)

A.超巨星　　　　　　　　　　 B.脉冲星核　　　　　 C.中子星　　　　　　　　　　 D.金属锇

1.一块冰融化成水以后，下列叙述中正确的是(　　 )

A.质量、体积、密度都变大　　　　　　　　　　 B.质量、体积、密度都变小

C.质量、体积、密度都不变　　　　　　　　　　 D.质量不变，体积变小，密度变大

5.测密度

(1)测固体的密度

固体的质量可直接用天平测得，外形不规则物体的体积可通过“排水法”来测量.然后根据密度公式ρ=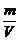求出密度.

说明　 ①如果待测物体不溶入水且密度比水小(如蜡)，测量其体积采取的办法有两种，一是悬锤法：将悬挂的石块或铁块浸入量筒内的水中，记下示数V₁，再将密度比水小的待测物体与石块或铁块连在一起浸入水中，记下此时水面示数V₂，待测物体的体积为V₂-V₁；二是针压法：用一细针刺入待测物，将待测物浸入水中后，用力压细针，把待测物全部压入水中，忽略针尖的体积，通过观察水面上升刻度的变化，便可求出待测物的体积；

②如果待测物尺寸大于量杯或量筒的口径，可以借助溢水杯，将待测物浸入盛满水的溢水杯中，再用量筒或量杯量出从溢水杯中溢出水的体积，便是待测物的体积；

(2)测液体的密度

液体的体积可以直接用量筒(或量杯)测出，其质量可通过“补差法”来测定，即先测出容器的质量，再测出容器与液体的总质量，两者之差就是容器内液体的质量，再根据ρ=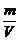求得密度.

[例3]　 (江苏无锡市中考题)为了鉴别某金属块的材料，先将该金属块放在调好的天平上，测出它的质量，然后将它放进盛有水的量筒内，测出它的体积.天平平衡时右盘中的砝码和游码的示数以及量筒中水面先后的位置如图2.3-2所示.该金属块的质量是　　　　　　　 g，它的体积是　　　　　　　　　 cm³，算出它的密度后查表可知该金属可能是　　　　　　　　 .

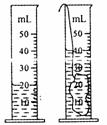
图2.3-2

思路与技巧 　测不规则形状固体的密度时，用天平称出物体质量，用排水法测体积，然后用公式ρ=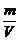计算密度.

答案　 54g　 20cm³　　　 　 铝.

[例4]　 (2004·黄冈市)小华同学在测定食用色拉油的密度的实验中，其方法步骤完全正确.图2.3-3显示的是他测量的相关数据，请帮小华填写下表中空白测量量和数据.

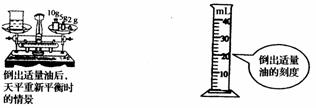
图2.3-3

思路与技巧 　本题考查的是测液体密度的实验，但主要考查的是读数记录和数据处理的能力.倒出油后烧杯与油的总质量读数为17.0 g，油的体积读数为20.0cm³，故油密度为0.84 ×10³ kg／m³.

答案　 33.8　 　17.0 g　 　油的体积　 20.0cm³　　 0.84.

探究体验

试一试，动手自制“鸡尾酒”.

探究器材　 试管、酒精、水、泛乳白色的机油、(红、蓝)墨水、软木塞

探究过程　 ①将试管洗净，倒入染红的水；

②沿管壁慢慢倒入的油；

③再沿管壁慢慢倒入蓝墨水的染色后酒精；

④用软木塞塞紧管口，管内形成了三色液柱，颠倒试管，三色液柱不变.如图2.3-4.

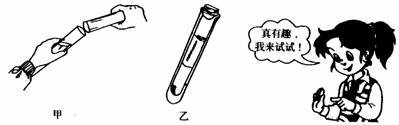
图2.3-4

分析与结论 　由于水、机油、酒精的　　　　　　　　　　 不同，因而它们分布在不同深度.实验中应注意　　　　　　　　　　 .

探究点拨 　认真、细致是实验操作的基本要求.

[例5]　 由于黄河上游水土流失，导致黄河水中含沙量增加，为了及时监测其含沙量，现在某河段中间捞取体积为5×10^-3m³黄河水，测得其质量为 5.6kg，问该河段每立方米黄河水(指纯水和沙的总体积为1m³)中的含沙量为多少kg(沙的密度为2.5×10³kg/m³)？

思路与技巧　 在某河段捞取质量为5.6 kg、体积为5×10^-3m³的黄河水，是指纯水和沙的总质量为5.6kg、总体积为5×10^-3m³.然后根据公式m=ρV和V=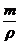可求出捞取的黄河水的含沙量，再求出1m³黄河水的含沙量.

答案 　设 5×10^-3m³的黄河水中含有水和沙的体积分别为V_水和V_沙，设5.6kg的黄河水中含有水和沙的质量分别为m_水和m_沙则有：

m_水+m_沙=m　　　　　 V_水+V_沙＝V

然后将V_水=，V_沙=代入整理得：

m_沙= 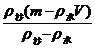=kg=1kg

所以1m³黄河水中含沙量

　M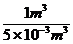＝×1kg＝200kg.

聊天室

话题：谁是密度大王？

胖胖：老师，世界上哪一种物质的密度最大？

老师：在地球上，密度最大的是金属锇，它的密度为22.5×10³kg/m³.但是在茫茫的宇宙中，金属锇简直是“密度家族”中的小不点.天空中的白矮星，个子不大，密度却大得惊人，为水的密度的3600万到几亿倍.

1957年，天文工作者用望远镜发现了中子星，它的密度高达1.0×10¹⁷kg/m³.一个火柴盒那么大的一块中子星物质，有 30亿吨的质量，要用九万六千多台重型火车头才能拉动它，

宇宙中还有一种新天体，密度比中子星还大，高达1.82×10¹⁹kg/m³，它对其他物体的吸引力非常大，只要被它吸引就会吞没，甚至连光也不放过，因为它不发光，人们给它取了个形象的名字叫“黑洞”.如图2.3-5.

图2.3-5

快乐套餐

4.密度知识的应用

由密度公式变形可得m=ρV和V=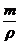两个公式.这三个公式代表密度知识有三个方面的应用.

(1)计算物体的质量.对于不便于直接测质量的物体，只要知道这个物体是由什么物质组成的，就可通过查密度表，查出这种物质的密度，再想办法测算出它的体积，根据公式m＝ρV，就能算出该物体的质量.如，要测算一块大理石碑的质量，大理石的密度可以查表得到，大理石的长、宽、高可以用刻度尺测量，算出大理石的体积，应用公式m=ρV，就可算出大理石的质量；

(2)计算物体的体积.对于不便于直接测量体积的物体，如形状不规则的铁制螺钉，可以用天平测量出螺钉的质量，铁的密度可以从密度表中查出，根据公式V=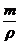，就可算出螺钉的体积；

(3)鉴别物质.根据公式ρ=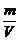.要知道一个物体是什么物质做的，只要测出它的密度，再查阅密度表，看测得的密度值与何种物质的密度相近.如测算出某物质的密度是2.6×10³kg／m³，通过查密度表，知道这种物质是花岗岩.

[例2]　 我国古典名著《西游记》中，齐天大圣孙悟空用来降妖除魔的如意金箍棒本来是东海中的一根“定海神针”(如图2.3-1).书中写道：“该棒长两丈多，斗来粗细，有13500斤.”其体积用国际单位表示大约是0.86 m³.

图2.3-1

(1)计算一下如意金箍棒的密度是多大？可能用地球上的什么物质做成？

(2)这金箍棒可以随意变化，当孙悟空挥动它除妖魔时，它的体积只有原来的二十分之一，而目前已知地球上密度最大的物质是金属锇，密度是2.25×10⁴kg/m³.地球上此时有做成金箍棒的物质吗？

思路与技巧 　根据ρ=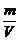即可算出金箍棒的密度，从而鉴别其是由何种物质做成的；若金箍棒的体积缩小到原来的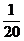，但质量不变，金箍棒的密度将增大为原来的20倍.

答案 　(1)金箍棒的密度ρ=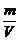=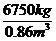≈7.85×10³kg／m³，可能是地球上的钢铁制成的

(2)此时金箍棒的体积为V′=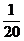V=0. 043 m³，而质量m保持不变，则此时金箍棒的密度ρ′=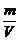=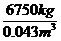≈ 15.7×10⁴kg/m³＞2.25×10⁴kg/m³.故地球上没有此物质.

3.密度的单位

国际单位是千克/米³(kg/m³)，常用单位有克/厘米³(g／cm³)，它们之间的换算关系：1g/cm³＝10³kg/m³.