
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题记分。作答时,先用2B铅 笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。K^S*5U.C#O%
笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。K^S*5U.C#O%
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵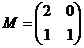 :(1)求矩阵
:(1)求矩阵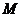 的逆矩阵
的逆矩阵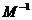 ;
;
(2)求矩阵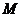 的特征值及相应的特征向量
的特征值及相应的特征向量
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知曲线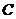 的极坐标方程为
的极坐标方程为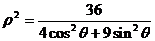 ;
;
(1)若以极点为原点,极轴所在的直线为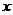 轴,求曲线
轴,求曲线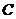 的直角坐标方程;
的直角坐标方程;
(2)若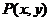 是曲线
是曲线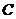 上的一个动点,求
上的一个动点,求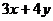 的最大值
的最大值
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数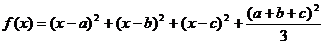 (
(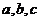 为实数)
为实数)
(1)求 的最小值
的最小值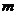 (用
(用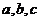 表示)
表示)
(2)若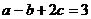 ,求(1)中
,求(1)中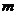 的最小值。
的最小值。
2010年泉州一中高三适应性测试数学(理科)试题2010.5
20.(本小 题满分14分)
题满分14分)
已知函数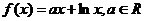 。
。
(1)求函数 的极值;
的极值;
(2)对于曲线上的不同两点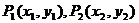 ,如果存在曲线上的点
,如果存在曲线上的点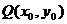 , 且
, 且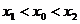 ,使得曲线在点
,使得曲线在点 处的切线
处的切线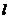 ∥
∥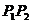 ,,则称
,,则称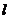 为弦
为弦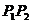 ,的伴随切线。
,的伴随切线。
特别地,当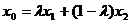
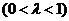 时,又称
时,又称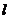 为弦
为弦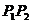 ,的
,的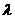 -伴随切线。
-伴随切线。
①求证:曲线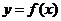 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
②是否存在曲线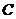 ,使得曲线
,使得曲线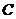 的任意一条弦均有
的任意一条弦均有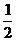 -伴随切线?若存在,给出一条这
-伴随切线?若存在,给出一条这
样的曲线,并证明你的结 论;若不存在,说明理由。
论;若不存在,说明理由。
19.(本小题满分13分)
已知抛物线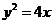 ,点
,点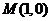 关于
关于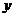 轴的对称点为
轴的对称点为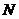 ,直线
,直线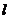 过点
过点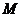 交抛物线于
交抛物线于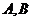 两点.
两点.
(1)证明:直线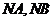 的斜率互为相反数;
的斜率互为相反数;
(2)求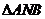 面积的最小值;
面积的最小值;
(3)当点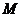 的坐标为
的坐标为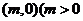 ,且
,且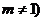 .根据(1)(2)结论试推测并回答下列问题(不必说明理由):
.根据(1)(2)结论试推测并回答下列问题(不必说明理由):
① 直线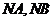 的斜率是否仍互为相反数?
的斜率是否仍互为相反数?
② 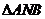 面积的最小值是多少?
面积的最小值是多少?
18.(本小题满分13分)
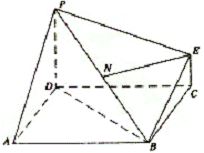 右图为一简单组合体,其底面
右图为一简单组合体,其底面 为正方形,
为正方形,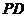
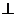 平面
平面 ,
,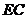 //
//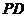 ,且
,且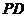 =
=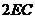 。K^S*5U.C#O%
。K^S*5U.C#O%
(1) 求证:
求证: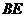 //平面
//平面 ;
;
(2)若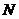 为线段
为线段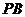 的中点,
的中点,
求证: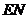
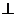 平
平 面
面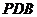 ;
;
(3)若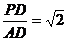 ,求平面
,求平面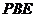 与平面
与平面
所成的二面角的大小。
17.(本小题满分1 3分)
3分)
已知函数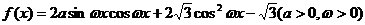 的最大值为
的最大值为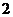 ,
,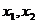 是集合
是集合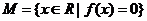 中的任意两个元素,且|
中的任意两个元素,且|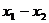 |的最小值为
|的最小值为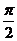 。
。
(1)求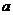 ,
,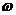 的值;
的值;
(2)若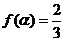 ,求
,求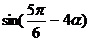 的值
的值
16. (本小题满分13分)
(本小题满分13分)
某地区有甲,乙,丙三个单位招聘工作人员,已知一大学生到这三个单位应聘的概率分别是0.4,0.5,0.6,且他是否去哪个单位应聘互不影响,用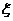 表示他去应聘过的单位数
表示他去应聘过的单位数
(1)求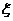 的分布列及数学期望;
的分布列及数学期望;
(2)记“数列 (
(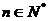 )是严格单调
)是严格单调 的数列”为事件
的数列”为事件 ,求事件
,求事件 发生的概率。
发生的概率。
15.在平面上有如下命题:“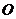 为直线
为直线 外的一点,则点
外的一点,则点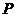 在直线
在直线 上的充要条件是:存在实数
上的充要条件是:存在实数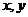 满足
满足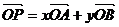 ,且
,且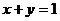 ”,我们把它称为平面中三点共线
”,我们把它称为平面中三点共线 定理,请尝试类比此命题,给出空间中四点共面定理,应描述为:
定理,请尝试类比此命题,给出空间中四点共面定理,应描述为:

14.当实数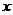 满足约束条件
满足约束条件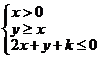 (其中
(其中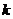 为小于零的常数)时,
为小于零的常数)时,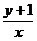 的最小值为
的最小值为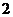 ,则实数
,则实数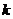 的值是
的值是
 .
.
13.按如右上图所示的程序框图运算,若输出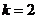 ,则输入
,则输入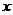 的取值范围是______ .
的取值范围是______ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com