
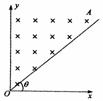
49.如图所示,在坐标系的第Ⅰ象限内有一匀强磁场区域,磁感应强度为B,y轴是磁场左侧的边界,直线OA是磁场的右侧边界。在第Ⅱ象限的区域,有一束带正电的粒子(重力不计)垂直y轴射入磁场,粒子的质量为m,带电量为q,粒子在各入射点的速度与入射点的y轴坐标值成正比,即v = by(b是常数,且b > 0)。要求粒子穿过磁场区域后,都垂直于x轴射出,求:直线OA与x轴的夹角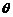 多大(用题中已知物理量的符号表示)?
多大(用题中已知物理量的符号表示)?
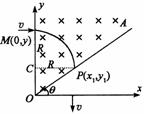 答案:在y轴上的M
(0,y)点入射的一粒子,其速度v = by,进入磁场后,做圆周运动,在右侧边界的P点射出时速度方向垂直x轴,因此圆周的圆心在y轴上的C点,如图所示。
答案:在y轴上的M
(0,y)点入射的一粒子,其速度v = by,进入磁场后,做圆周运动,在右侧边界的P点射出时速度方向垂直x轴,因此圆周的圆心在y轴上的C点,如图所示。
根据qvB
= m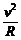
得圆周半径R =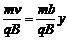
设P点的坐标为(x1,y1),由图可得
tan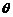 =
=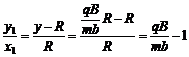
即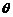 = arctan
= arctan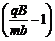
48.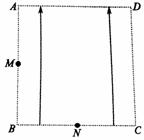 如图所示,匀强电场分布在正方形ABCD区域内,M、N分别为AB边和BC边的中点。一个具有初动能为E0的带电粒子射入电场(不沿纸面运动)。如果带电粒子从M点垂直于电场方向进入电场后,恰好从D点离开电场。带电粒子重力不计,试回答下列问题:
如图所示,匀强电场分布在正方形ABCD区域内,M、N分别为AB边和BC边的中点。一个具有初动能为E0的带电粒子射入电场(不沿纸面运动)。如果带电粒子从M点垂直于电场方向进入电场后,恰好从D点离开电场。带电粒子重力不计,试回答下列问题:
(1)带电粒子从D点离开电场时的动能是多大?
(2)如果带电粒子从N点垂直于BC边方向射入电场,它离开电场时的动能又是多大?
答案:设带电粒子的质量为m、电量为q、初速度为v(E0 =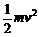 ),正方形边长为L,匀强电场的电场强度为E。
),正方形边长为L,匀强电场的电场强度为E。
带电粒子从M点垂直于电场方向进入电场后做类平抛运动。从D点离开电场,说明粒子带正电,沿电场方向的位移为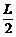 。
。
有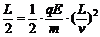 得qEL = mv2 = 2E0
得qEL = mv2 = 2E0
带电粒子从M点射入,从D点射出,电场力做功W = qE ·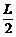 = E0,设带电粒子从D点离开电场时的动能为E1,根据动能定理有W = E1 – E0,故E1 = W + E0 =
2E0。
= E0,设带电粒子从D点离开电场时的动能为E1,根据动能定理有W = E1 – E0,故E1 = W + E0 =
2E0。
(2)带电粒子从N点沿垂直于BC边方向射入电场,做匀加速直线运动,设离开电场时的动能为E2,根据动能定理得qEL = E2 – E0,得E2 = E0 + qEL = 3E0。
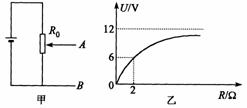
47.一个允许通过电流为2 A的电源和一个滑动变阻器,接成如图甲所示的电路。变阻器最大阻值为R0 = 22Ω,电源路端电压U随外电阻R变化的规律如图乙所示,图中U = 12V的直线为图象的渐近线,试求:
(1)电源电动势和内电阻;
(2)A、B空载时输出电压的范围;
(3)若要保证变阻器的滑片能任意滑动,A、B两端所接负载的最小电阻为多大?
答案:(1)由乙图可知,当R→∞时,E = Um = 12V
而当U =
6V = 时,应有r = R = 2Ω
时,应有r = R = 2Ω
(2)当滑片滑至最上端时,UAB最大
Umax
=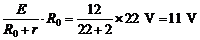
当滑片滑至最下端时,UAB最小:Umin = 0
因此,A、B空载时输出电压的范围为0 ~ 11 V
(3)当A、B接负载电阻Rx后,变阻器滑片移至最上端时,干路电流最大,
此时:I
=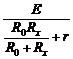
为了电源不过载,应保证:I ≤Im = 2 A,代入数据解得:Rx≥4.9Ω
46.在如图所示的电路中,电池的电动势E = 5 V、内电阻r = 10Ω,固定电阻R = 90Ω,R0是可变电阻,在R0由零增加到400Ω的过程中,求
(1)可变电阻R0上消耗热功率最大的条件和最大热功率。
(2)电池的内电阻r和固定电阻R上消耗的最小热功率之和。
答案:(1)由闭合电路欧姆定律可得,电路中的电流I =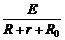 ,则可变电阻R0上消耗的热功率
,则可变电阻R0上消耗的热功率
P1
= I2R0 =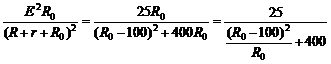
显然,当R0 = 100Ω时,P1最大,
P1
max =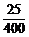 W = 6.25 × 10 – 2 W
W = 6.25 × 10 – 2 W
亦可利用等效法求解,即将电源的内阻等效为r + R,当R0 = R + r = 100Ω时,等效电源的输出功率P1最大。
(2)r和R消耗的热功率
P2
= I2(R + r)=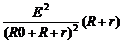
当R0 = 400Ω时,即R0最大时P2最小
P2min
=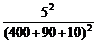 ×(90 + 10)W = 0.01 W
×(90 + 10)W = 0.01 W
45.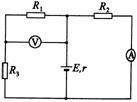 如图所示的电路中,电阻R1 = R3
= 4Ω,两电表均为理想电表。电流表的示数为0.50 A,电压表的示数为2.0 V。由于某种原因电路中有一只电阻发生断路,使电流表的读数变为0.60 A,电压表的读数变为4.8 V。问:
如图所示的电路中,电阻R1 = R3
= 4Ω,两电表均为理想电表。电流表的示数为0.50 A,电压表的示数为2.0 V。由于某种原因电路中有一只电阻发生断路,使电流表的读数变为0.60 A,电压表的读数变为4.8 V。问:
(1)哪一只电阻发生了断路?为什么?
(2)电阻R2的阻值为多少?
(3)电源的电动势和内阻分别是多少?
答案:(1)若R3处断路,则电压表无示数;若R2处断路,则电流表无示数。综上可知,只能是R1处断路。
(2)R1处断路后,电压表的示数就是R2两端的电压。
∴R2 =
(3)当I2 = 0.5 A时,U外 = U1 + U3 = 2 + 2 = 4(V)
I总 = I1 + I2
=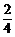 + 0.5 = 1.0(A)
+ 0.5 = 1.0(A)
由全电路欧姆定律列出:E = U外 + I总· r = 4 + r
由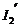 = 0.6 A时,
= 0.6 A时,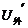 = 4.8 V,
= 4.8 V,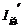 =
=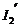 = 0.6 A
= 0.6 A
由全电路欧姆定律列出:E = U外 + 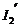 r = 4.8 + 0.6 r
r = 4.8 + 0.6 r
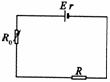 解得r =
2.0Ω,E = 6.0 V。
解得r =
2.0Ω,E = 6.0 V。
44.地球绕太阳运行的轨道可以认为是圆形的,已知地球的半径为R,地球赤道表面的重力加速度为g,地球绕太阳运转的周期为T,从太阳发出的光经过时间t0到达地球,光在空气中的传播速度为c。根据以上条件推算太阳的质量M与地球的质量m之比 为多大。
为多大。
答案:地球绕太阳做匀速圆周运动,设运动半径为r,角速度为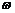 ,有
,有
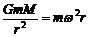 ,
,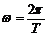 ,r = ct0
,r = ct0
设地球赤道上小物体的质量为m0,有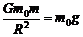
由以上各式得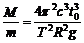 。
。
43.假设若干年后,宇航员站在了火星表面。宇航员要乘坐返回舱返回距离火星中心r的轨道舱(围绕火星运动的舱体)。为了安全,返回舱与轨道舱对接时,必须具有相同的速度。如果宇航员在火星上时,自头顶自由释放一个小球,经时间t,小球恰好落到火星表面。且已知火星的半径为R,万有引力常量为G,宇航员的高为h,返回舱与人的总质量为m,返回过程中需克服火星引力做功W = mgR (–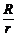 ),g为火星表面的重力加速度。不计火星表面大气及火星自转的影响。求:
),g为火星表面的重力加速度。不计火星表面大气及火星自转的影响。求:
(1)火星表面的重力加速度g;
(2)宇航员乘坐返回舱返回轨道舱的过程中消耗的总能量。
答案:(1)小球在火星表面做自由落体运动h =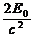
得:g =
(2)在火星表面附近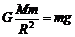
得:GM = gR2
轨道舱做圆周运动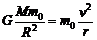
其中m0为轨道舱的质量,v为轨道舱的速度大小
返回舱与轨道舱对接时的动能为Ek =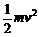
返回舱返回过程中克服引力做功W = mgR (1–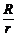 )
)
返回舱返回过程中消耗的总能量E = Ek + W =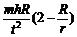 。
。
42.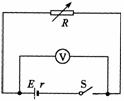 要求测量由2节干电池串联而成的电池组的电动势E和内阻r(约几欧),提供下列器材:电压表V1(量程3V,内阻1 kΩ)、电压表V2(量程10V,内阻2 kΩ)、电阻箱(0 ~ 9
999Ω)、开关、导线若干
要求测量由2节干电池串联而成的电池组的电动势E和内阻r(约几欧),提供下列器材:电压表V1(量程3V,内阻1 kΩ)、电压表V2(量程10V,内阻2 kΩ)、电阻箱(0 ~ 9
999Ω)、开关、导线若干
某同学用量程为10 V的电压表连接成如图所示的电路,实验步骤如下:
(1)合上开关S,将电阻箱R阻值箱R阻值调到R1 = 10Ω,读得电压表的读数为U1;
(2)将电阻箱R阻值调到R2 = 20Ω,读得电压表的读数为U2,由方程组U1 = E –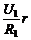 ,U2 = E
–
,U2 = E
–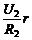 ,解出E、r,为了减少实验误差,上述实验在选择器材和实验步骤中,应做哪些改进?_____________________________。
,解出E、r,为了减少实验误差,上述实验在选择器材和实验步骤中,应做哪些改进?_____________________________。
答案:在选择器材上,选用量程为10V的电压表会使测量误差过大,因2节干电池的电动势约3V左右,所以应选择电压表V1。
本题更注重的是实验步骤的改进,力求尽可能减小实验测量中带来的误差,故应改变电阻箱阻值R,读取若干个U值。
41.从下表中选出适当的实验器材,设计一电路来测量电流表A1的内阻r1,要求方法简捷,测量精度较高,并能测得多组数据。
|
器材代号 |
规格 |
|
电流表(A1) |
量程10 mA,内阻r1待测(约40Ω) |
|
电流表(A2) |
量程500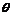 A,内阻r2
= 750Ω A,内阻r2
= 750Ω |
|
电压表(V) |
量程10 V,内阻r3 = 10 kΩ |
|
电阻(R1) |
阻值约100Ω,作保护电阻用 |
|
滑动变阻器(R2) |
总阻值约50 |
|
电池(E) |
电动势1.5 V,内阻很小 |
|
电键(S) |
|
|
导线若干 |
|
(1)画出电路图,标明所用器材的代号。
(2)若选测量数据中的一组来计算r1,则所用的表达式r1 = ________,式中各符号的意义是_________________________。
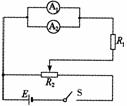 答案:(1)
答案:(1)
(2)r1 =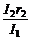 。式中I2为通过电流表A2的电流,r2为电流表A2的内阻,I1为通过电流表A1的电流。
。式中I2为通过电流表A2的电流,r2为电流表A2的内阻,I1为通过电流表A1的电流。
40.有一根细而均匀的导电材料样品,截面为同心圆环,如右图所示,此样品长L约为3 cm,电阻约为100Ω,已知这种材料的电阻率为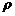 ,因该样品的内径太小,无法直接测量。现提供以下实验器材:
,因该样品的内径太小,无法直接测量。现提供以下实验器材:
 A.20等分刻度的游标卡尺
A.20等分刻度的游标卡尺
B.螺旋测微器
C.电流表A1(量程50 mA,内阻的准确值r1为100Ω)
D.电流表A2(量程100 mA,内阻r2大约为40Ω)
E.滑动变阻器R1(0 ~ 10Ω,额定电流2 A)
F.直流电流E(12 V,内阻很小)
G.导电材料样品R2(长L约为3 cm,电阻R2约为100Ω)
H.电键一只,导线若干
请根据上述器材设计一个尽可能精确地测量该样品内径d的实验方案,回答下列问题:
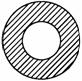
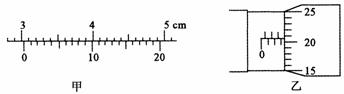
(1)用游标卡尺测得该样品的长度如图甲所示,其示数L = ________;用螺旋测微器测得该样品的外径如图乙所示,其示数D = _________。
(2)在下面的方框中画出设计的实验电路图,并标明所选器材前的字母代号。

(3)用已知物理量和所测得物理量的符号表示样品的内径d,并写出推导过程。
答案:(1)30.35 mm 3.205 ~ 3.208 mm
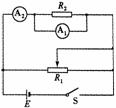 (2)电路如右图所示
(2)电路如右图所示
(3)设电流表A1、A2的示数分别为I1、I2,则
I1 · r1 = (I2 – I2) · R2
由电阻定律R2 =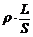
由几何知识S =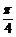 (D2 – d2)
(D2 – d2)
联立以上各式解得d =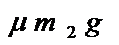 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com