
59.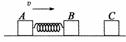 用轻弹簧相连的质量均为2 kg的A、B两物块都以v = 6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量为4 kg的物体C静止在前方,如图所示,B与C碰撞后二者粘在一起运动。求:在以后的运动中,
用轻弹簧相连的质量均为2 kg的A、B两物块都以v = 6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量为4 kg的物体C静止在前方,如图所示,B与C碰撞后二者粘在一起运动。求:在以后的运动中,
(1)当弹簧的弹性势能最大时物体A的速度多大?
(2)弹性势能的最大值是多大?
(3)A的速度有可能向左吗?为什么?
答案:(1)当A、B、C三者的速度相等时弹簧的弹性势能最大,由于A、B、C三者组成的系统动量守恒,有(mA + mB)v =(mA + mB + mC)vA
解得vA =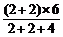 = 3(m/s)
= 3(m/s)
(2)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为 ,
,
则mBv = (mB + mc) ,
,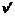 =
=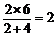 (m/s)
(m/s)
设物块A速度为vA时弹簧的弹性势能最大为Ep,根据能量守恒
Ep = 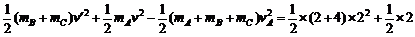 × 62
× 62
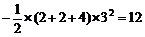 (J)
(J)
(3)由系统动量守恒得
mAv + mBv = mAvA + (mB + mC) vB
设A的速度方向向左,vA < 0,则mB > 4 m/s
则作用后A、B、C动能之和
Ek
=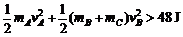
实际上系统的机械能
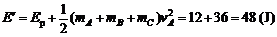
根据能量守恒定律,Ek >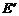 是不可能的。故A不可能向左运动。
是不可能的。故A不可能向左运动。
58.如图所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平,一个质量为m的物体P从轨道顶端A处由静止释放,滑到B端后飞出,然后落到地面的C点,其轨迹如图中虚线BC所示。已知它落地时相对于B点的水平位移OC = l。现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为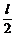 。当传送带静止时,让物体P再次从A点静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落到地面的C点。当驱动轮转动带动传送带以速度v匀速向右运动(其他条件不变),物体P的落地点为D,问传送带速度v的大小满足什么条件时,OD间的距离s有最小值?这个最小值为多少?
。当传送带静止时,让物体P再次从A点静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落到地面的C点。当驱动轮转动带动传送带以速度v匀速向右运动(其他条件不变),物体P的落地点为D,问传送带速度v的大小满足什么条件时,OD间的距离s有最小值?这个最小值为多少?
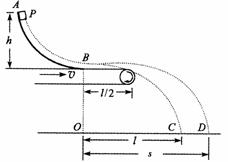
答案:物体P从轨道底端或从传送带右端滑出均做平抛运动。因为两个端点离地面的高度相等,所以平抛运动的水平射程与初速度成正比,即
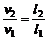
由题意可知,l2 =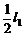 ,v1 =
,v1 =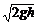 ,故得v2 =
,故得v2 =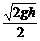
物体P在传送带上滑动时,滑动摩擦力做负功,由动能定理得
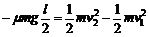
进而解得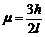
当传送带向右运动时,要使小物体的水平射程最小,必须使它到达传送带右端时速度最小,这就要求P在传送带上一直做减速运动,那么传送带的速度只要小于或等于前面所计算的P在静止的传送带上滑至右端的速度v2。这样,物体P离开传送带的速度为v2,即传送带的速度v≤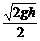 时,OD间的距离最小为smin = l。
时,OD间的距离最小为smin = l。
57.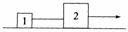 如图所示。1、2两木块用短钩相连,放在水平地面上。1和2两木块的质量分别是m1 = 1.0 kg和m2 = 2.0 kg。它们与水平地面间的动摩擦因数均为
如图所示。1、2两木块用短钩相连,放在水平地面上。1和2两木块的质量分别是m1 = 1.0 kg和m2 = 2.0 kg。它们与水平地面间的动摩擦因数均为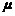 = 0.10。在t = 0秒时开始用向右的水平恒力F = 6.0 N拉木块2。过一段时间后短钩脱开,到t = 6.0 s时1、2两木块相距s = 4.0 m,木块1早已停住。求此时木块2的速度。
= 0.10。在t = 0秒时开始用向右的水平恒力F = 6.0 N拉木块2。过一段时间后短钩脱开,到t = 6.0 s时1、2两木块相距s = 4.0 m,木块1早已停住。求此时木块2的速度。
答案:设脱钩的时刻为t1,此时两木块的速度为v1,由动量定理得
Ft1
–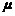 (m1 + m2) gt1
= (m1 + m2) v1 ①
(m1 + m2) gt1
= (m1 + m2) v1 ①
脱勾后,由于摩擦力作用,木块1在水平地面上滑动了s1后停住,由动能定理得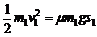 ②
②
木块2从脱钩到t = 6.0 s所经过的时间为t2 = (t – t1),设在此时间段内,木块2滑行的距离为s2,在t = 0.6 s时刻的速度为v2,由动能定理得
 ③
③
由动量定理得
m2v2
– m2v1 = (F –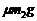 )(t – t1) ④
)(t – t1) ④
由题目所给条件得s2 – s1 = s ⑤
解① ~ ⑤式得v2 = 8.0 m/s
56.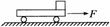 如图所示,平板小车M的质量为2 kg,放在足够长的光滑水平面上,质量为0.5 kg的小物块m(可视为质点)放在小车的右端,物块m与小车M间的动摩擦因数为0.2,开始时m、M均静止,当用大小为6 N的水平力F作用在小车上时,m、M立即发生相对滑动,水平力F作用0.5 s后撤去,g取10 m/s2。求:
如图所示,平板小车M的质量为2 kg,放在足够长的光滑水平面上,质量为0.5 kg的小物块m(可视为质点)放在小车的右端,物块m与小车M间的动摩擦因数为0.2,开始时m、M均静止,当用大小为6 N的水平力F作用在小车上时,m、M立即发生相对滑动,水平力F作用0.5 s后撤去,g取10 m/s2。求:
(1)当力F作用在小车上时,小车的加速为多大?
(2)当物块m的速度为1.1 m/s时,小车M的速度为多大?
(3)设小车长为0.5 m,则m是否会滑离M?若m会滑离M,求滑离时两者的速度;若m不会滑离M,求m最终在小车上的位置(以m离M右端的距离表示)。
答案:(1)对M : F –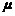 mg = Ma1,得
mg = Ma1,得
a1
=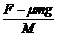 = 2.5 m/s2
= 2.5 m/s2
(2)对m :
a2 =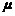 g = 2 m/s2
g = 2 m/s2
撤去F时,对M : v1 = a1t = 1.25 m/s
对m有v2 = a2t = 1 m/s
撤去F后,系统动量守恒Mv1 + mv2 =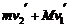 且
且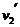 = 1.1 m/s
= 1.1 m/s
得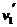 = 1.225 m/s
= 1.225 m/s
(3)在力F作用下的0.5 s内,M位移
s1
=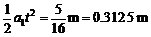
m位移s2 =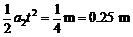
相对位移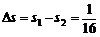 m = 0.062 5 m
m = 0.062 5 m
假设m不会离开M,撤去F后,二者达共同速度v,则
Mv1 + mv2 = (M + m) v得v = 1.2 m/s
设这一过程相对位移为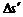 ,则
,则
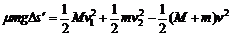
∴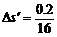 m = 0.012 5 m
m = 0.012 5 m
∴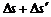 = 0.75 m
< L = 0.5 m
= 0.75 m
< L = 0.5 m
∴m不会离开M,最终m在距离M右端0.075 m处与M一起匀速运动。
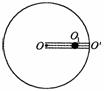
55.如图在水平圆盘上有一过圆心的光滑小槽,槽内有两根原长、劲度系数均相同的橡皮绳拉住一质量为m的小球,其中O点为圆盘的中心,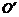 点为圆盘的边缘,O1为小球。橡皮绳的劲度系数为k,原长为圆盘半径R 的
点为圆盘的边缘,O1为小球。橡皮绳的劲度系数为k,原长为圆盘半径R 的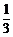 。现使圆盘角速度由零缓慢增大,求圆盘的角速度
。现使圆盘角速度由零缓慢增大,求圆盘的角速度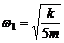 与
与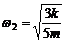 时,小球所对应的线速度之比v1 : v2
= ?
时,小球所对应的线速度之比v1 : v2
= ?
答案:当橡皮绳OO1被拉伸而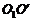 刚好被拉直时,设小球做匀速圆周运动角速度为
刚好被拉直时,设小球做匀速圆周运动角速度为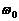 。
。
由牛顿第二定律有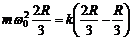 ,
,
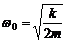 。
。
当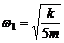 <
<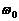 时,橡皮绳
时,橡皮绳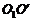 被拉伸,
被拉伸,
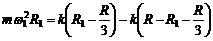 得R1 =
得R1 =
当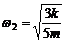 >
>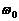 时,此时橡皮绳
时,此时橡皮绳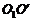 处于松驰状态
处于松驰状态
 ,得R2 =
,得R2 =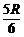
所以v1 : v2 =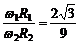
54. 如图所示,在水平方向的磁感应强度为B0的匀强磁场中竖直放置两宽度为L的平行导轨,磁场方向与导轨所在平面垂直。导轨上端跨接一阻值为R的电阻,导轨电阻不计。两金属棒a和b的电阻都为R,质量分别为ma = 20 g和mb = 10 g,它们与导轨相连,并可沿导轨无摩擦地滑动。闭合开关S,先固定b,用一恒力F向上拉a,稳定后,a以v1 = 10 m/s的速度匀速运动,此时再释放b,b正好能保持静止,g = 10 m/s2,导轨足够长。
如图所示,在水平方向的磁感应强度为B0的匀强磁场中竖直放置两宽度为L的平行导轨,磁场方向与导轨所在平面垂直。导轨上端跨接一阻值为R的电阻,导轨电阻不计。两金属棒a和b的电阻都为R,质量分别为ma = 20 g和mb = 10 g,它们与导轨相连,并可沿导轨无摩擦地滑动。闭合开关S,先固定b,用一恒力F向上拉a,稳定后,a以v1 = 10 m/s的速度匀速运动,此时再释放b,b正好能保持静止,g = 10 m/s2,导轨足够长。
(1)求拉力F的大小;
(2)若固定金属棒a,让金属棒b自由下滑(开关仍闭合),b滑行的最大速度v2为多大?
(3)若断开开关,将金属棒a和b都固定,使磁感应强度从B0随时间均匀增加,经0.1 s后磁感应强度增加到2B0时,a棒受安培力正好等于a棒的重力,求两棒间的距离h。
答案:(1)a杆切割磁感线相当于电源,电阻R与b杆并联
对a杆有:F = mag + B0IaL ①
对b杆有:mbg =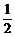 B0IaL ②
B0IaL ②
联立①②得F = 0.4 N
(2)当a以v1匀速上升时
Ea = B0Lv1 ③
Ia
=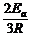 ④
④
联立②③④得v1 =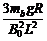
当b匀速运动时Eb = B0Lv2 ⑤
Ib
=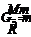 ⑥
⑥
B0IbL = mbg ⑦
联立⑤⑥⑦得v2 =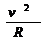
∴v2 =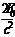 v1 = 5 m/s
v1 = 5 m/s
(3)此时感应电动势E =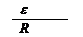 ,其中t = 0.1 s ⑧
,其中t = 0.1 s ⑧
电路中电流I =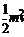 ⑨
⑨
当B = 2B0时,2B0IL = mag ⑩
∵v1 =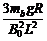 ,∴联立⑧⑨⑩得h =
,∴联立⑧⑨⑩得h =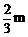
53.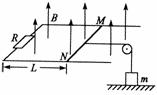 如图,不计电阻的U形导轨水平放置,导轨宽l = 0.5 m,左端连接阻值为0.4Ω的电阻R,在导轨上垂直于导轨放一电阻为0.1Ω的导体棒MN,并用水平轻绳通过定滑轮吊着质量m = 2.4 g的重物,图中L = 0.8 m,开始重物与水平地面接触并处于静止,整个装置处于竖直向上的匀强磁场中,此时磁感应强度B0 =
0.5 T,并且以
如图,不计电阻的U形导轨水平放置,导轨宽l = 0.5 m,左端连接阻值为0.4Ω的电阻R,在导轨上垂直于导轨放一电阻为0.1Ω的导体棒MN,并用水平轻绳通过定滑轮吊着质量m = 2.4 g的重物,图中L = 0.8 m,开始重物与水平地面接触并处于静止,整个装置处于竖直向上的匀强磁场中,此时磁感应强度B0 =
0.5 T,并且以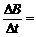 0.1 T/s的变化率在增大,不计摩擦阻力,求至少经过多长时间才能将重物吊起?(g = 10 m/s2)
0.1 T/s的变化率在增大,不计摩擦阻力,求至少经过多长时间才能将重物吊起?(g = 10 m/s2)
答案:以MN为研究对象,有BIl = T;以重物为研究对象,有T + N = mg。由于B在增大,安培力BIl增大,绳的拉力T增大,地面的支持力N减小,当N = 0,重物将被吊起。设将重物吊起需要的时间至少为t,此时BIl = mg,B = B0 +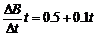
感应电动势E =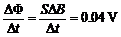
感应电流I
=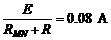
由以上各式求出t = 1 s。
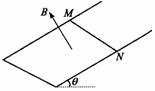
52.如图所示,足够长的U形导体框架的宽度L = 0.5 m,电阻忽略不计,其所在平面与水平面成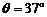 角,磁感应强度B = 0.8 T的匀强磁场方向垂直于导体框平面,一根质量m = 0.2
kg,有效电阻R = 2Ω的导体棒MN垂直跨放在U形框架上,该导体棒与框架间的动摩擦因数
角,磁感应强度B = 0.8 T的匀强磁场方向垂直于导体框平面,一根质量m = 0.2
kg,有效电阻R = 2Ω的导体棒MN垂直跨放在U形框架上,该导体棒与框架间的动摩擦因数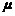 = 0.5。导体棒由静止开始沿框架下滑到刚开始匀速运动,通过导体棒截面的电量共为Q = 2 C。求:
= 0.5。导体棒由静止开始沿框架下滑到刚开始匀速运动,通过导体棒截面的电量共为Q = 2 C。求:
(1)导体棒匀速运动的速度;
(2)导体棒从开始下滑到刚开始匀速运动这一过程中,导体棒的有效电阻消耗的电功。(sin 37°= 0.6 cos 37°= 0.8 g = 10m/s2)
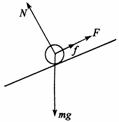
答案:(1)当导体棒匀速下滑时其受力情况如图:因为匀速下滑,设匀速下滑的速度为v,则:
平行斜面:mgsin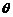 – f – F = 0
– f – F = 0
垂直斜面:N – mgcos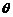 = 0
= 0
 其中:f
=
其中:f
=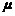 N
N
安培力:F = BIL
电流强度I
=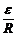
感应电动势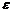 = BLv
= BLv
由以上各式得:v =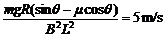
(2)通过导体的电量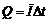
其中平均电流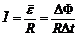
设物体下滑位移为s,则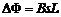
由以上各式得s =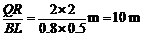
全程由动能定得:
mgs
· sin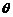 – W安 –
– W安 –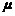 mgcos
mgcos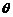 · s =
· s =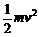
其中克服安培力做功W安等于导体棒的有效电阻消耗的电功W
则W = mgs
· sin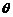 –
–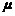 mgcos
mgcos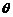 · s =
· s =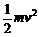 = (12 – 8 – 2.5) J = 1.5 J
= (12 – 8 – 2.5) J = 1.5 J
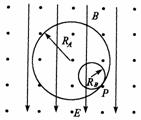
51.如右图所示的空间,存在着正交的匀强电场和匀强磁场。匀强电场的方向竖直向下,场强为E,匀强磁场的方向垂直纸面向外,磁感应强度为B。有两个带电小球A和B都能在垂直于磁场方向的同一竖直平面内做匀速圆周运动(两小球间的库仑力可忽略),运动轨迹如图。已知两个带电小球A和B的质量关系为mA = 3mB,轨道半径为RA = 3RB = 9cm。
(1)试说明小球A和B分别带什么电,并求出它们所带的电荷量之比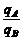 ;
;
(2)指出小球A和B的绕行方向,并求出它们的绕行速率之比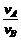 ;
;
(3)设带电小球A和B在图示位置P处相碰撞,且碰撞后原先在小圆轨道上运动的带电小球B恰好能沿大圆轨道运动,求带电小球A碰撞后做圆周运动的轨道半径(设碰撞时两个带电小球间电荷量不发生转移)。
答案:(1)因为两带电小球都在复合场中做匀速圆周运动,故必有qE = mg,由电场方向可知,两小球都带负电荷
因为mAg = qAE
mBg = qBE mA = 3mB,所以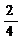 =
=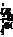
(2)由题意可知,两带电小球的绕行方向都相同,为逆时针
由qBv = 得R =
得R =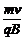 ,由题意RA = 3RB,所以
,由题意RA = 3RB,所以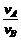 =
=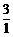
(3)由于两带电小球在P处相碰,切向合外力为零,故两带电小球在该处的切向运量定恒。
当mAvA + mBvB =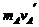 +
+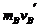 ,
,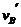 = vA = 3vB,得
= vA = 3vB,得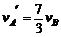
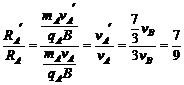
所以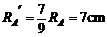
50.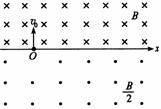 如右图,在x轴上方有磁感应强度大小为B,方向垂直纸面向里的匀强磁场。x轴下方有磁感应强度大小为
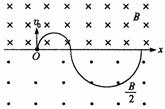
如右图,在x轴上方有磁感应强度大小为B,方向垂直纸面向里的匀强磁场。x轴下方有磁感应强度大小为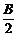 ,方向垂直纸面向外的匀强磁场。一质量为m、电量为– q的带电粒子(不计重力),从x轴上的O点以速度v0垂直x轴向上射出。求:
,方向垂直纸面向外的匀强磁场。一质量为m、电量为– q的带电粒子(不计重力),从x轴上的O点以速度v0垂直x轴向上射出。求:
(1)射出之后经多长时间粒子第二次到达x轴;
(2)粒子第二次到达x轴时离O点的距离。
答案:(1)粒子运动轨迹示意图如下图所示。
由牛顿第二定律得qv0B = m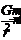 ①
①
 又T =
又T =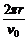 ②
②
依题意知B1 = B,B2 =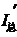 ③
③
由①③得T1 =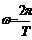 ,T2 =
,T2 =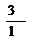
粒子第二次到达x轴所需时间
t =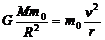
(2)由①式可知r1 =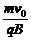 ,r2 =
,r2 =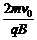
粒子第二次到达x轴时离O点的距离
 s
= 2r1 + 2r2 =
s
= 2r1 + 2r2 =
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com