22．(本小题满分14分)

　　 设函数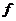(x)=x-，g(x)=2-+的定义域是x>0，若函数F(x)= 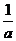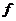(x)+g(x)有最小值m，且m>2+，求a的取值范围。

21．(本小题满分12分)

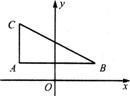
　　 如图，在Rt△ABC中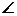，BAC=90°，A(-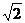，1)、B(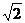，1)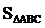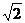， = (平方单位)，动点P在曲线E(y≥1)上运动．若曲线E过点C且满足|PA|+|PB|的值为常数。

(I)求曲线E的方程：

(Ⅱ)设直线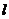的斜率为1，若直线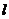与曲线E有两个不同的交点P、Q，求线段PQ的中点M的轨迹方程。

20．(本小题满分12分)

　　 某生产流水线．由于改进了设备，预计第一年产量的增长率为160%，以后每年的增长率是前一年的一半。设原来的产量是a。

　　 (I)写出改进设备后的第一年，第二年，第三年的产量，并写出第n年与第n-1年(n≥2，n∈N)的产量之间的关系式；

(Ⅱ)由于设备不断老化，估计每年将损失年产量的5%，如此下去，以后每年的产量是否始终是逐年提高?若是，请给予证明；若不是；请说明从第几年起，产量将比上一年减少?

19．(本小题满分12分，Ⅱ甲、Ⅱ乙两题请任选一题)

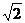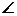　 在三棱锥P-ABC中，PA=a，AB=AC=a，PAB=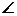PAC=45°，cos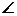BPC=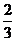

　 (I)D是AB上任意一点(D与A、B不重合)，DE⊥PB于E，求证AP∥平面DEC；

(Ⅱ甲)在(I)中，若D是AB的中点，求平面PAC与平面DEC所成二面角的余弦值。

　 (Ⅱ乙)在(I)中，若D是AB的中点，求cos<，>。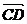

18．(本小题满分12分)

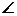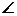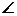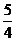已知△ABC中，A、B、C的对边分别是a、b、c，若COS (+A)+cosA=，b+c=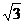a，求A、B、C的大小。

17．(本小题满分12分)

　　 已知函数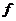(x)：log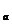 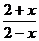　(0<a<1)。

(I)　　　　　　　 试判断函数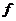(x)的奇偶性；

(Ⅱ)解不等式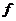(x)≥log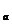3x。

16．某地区重视环境保护，绿色植被面积呈上升趋势，经调查，从1989年到1998年这10年间每两年上升2%，1997年和1998年这两年种植植被815×10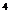 m，当地政府决定今后四年内仍按这一比例发展下去，那么从1999年到2002年种植植被面积为_______(保留整数)。

15．已知两异面直线a、b所成的角为，直线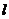分别与a、b所成的角都是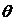，则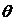的取值范围是_____________________。

14．设抛物线y=4x的一条弦AB以P(，1)为中点，则该弦所在直线的斜率为_______。

13．某高校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设，某人必须被选派的种数是________________。