3．以加速度a做匀加速直线运动的物体。速度从v增加到2v、从2v增加到4v、从4v增加到8V所需时间之比为_____________；对应时间内的位移之比为____________。

2．一个作匀加速直线运动的物体，通过A点的瞬时速度是v_l，通过B点的瞬时速度是V₂，那么它通过A、B中点的瞬时速度是　 (　　 )

A．　　　 B．　 C．　 D．

1．在初速为零的匀加速直线运动中，最初连续相等的四个时间间隔内的平均速度之比是 (　　 )

A．1：1：l：1　 B．1：3：5：7　　 C．1²：2²：3²：4²　 D．1³：2³：3³：4³

追及和相遇类问题的一般处理方法是：①通过对运动过程的分析，找到隐含条件(如速度相等时两车相距最远或最近)，再列方程求解。②根据两物体位移关系列方程，利用二次函数求极值的数学方法，找临界点，然后求解。

解这类问题时，应养成画运动过程示意图的习惯。画示意图可使运动过程直观明了，更能帮助理解题意，启迪思维。

　　 l、匀加速运动质点追匀速运动质点：

　　 设从同一位置，同一时间出发，匀速运动质点的速度为v，匀加速运动质点初速

　　 为零，加速度为a，则：

　　 (1)　 经t=v／a两质点相距最远

　　 (2)　 经t=2v／a两质点相遇

[例三]摩托车的最大速度为30m／s，当一辆以lOm／s速度行驶的汽车经过其所在位置时，摩托车立即启动，要想由静止开始在1分钟内追上汽车，至少要以多大的加速度行驶?摩托车追赶汽车的过程中，什么时刻两车距离最大?最大距离是多少?如果汽车是以25m／s速度行驶的，上述问题的结论如何?

2、匀减速运动质点追匀速运动质点：

设A质点以速度v沿x轴正向做匀速运动，B质点在A质点后方L处以初速v_o，

加速度a沿x正向做匀减速运动，则：

(1)　 B能追上A的条件是：

(2)　 B和A相遇一次的条件是；

(3)　 B和A相遇二次的条件是：

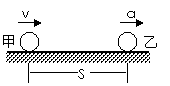[例四]如图所示；处于平直轨道上的甲、乙两物体相距为s，同时向右运动，甲以速度v做匀速运动，乙做初速为零的匀加速运动，加速度为a，试讨论在什么情况下甲与乙能相遇一次?在什么情况下能相遇两次?

课堂训练：

2．等分位移(以S为单位)

　　 (1)通过lS、2S、3S……所用时间之比为：

　　　　 t_l：t₂：t₃…=l：：…

　　 (2)通过第一个S、第二个S、第三个S……所用时间之比为：

　　　　 t_l：t₂：t₃…=l：(-1)：(一)…

　　 (3)lS末、2S末、3S末……的瞬时速度之比为：

　　　　 V₁：V₂：V₃…=l：：…

[例一]一质点做初速度为零的匀加速直线运动，它在第一秒内的位移是2米，那么质点在第lOs内的位移为多少?质点通过第三个2米所用的时间为多少?

[例二]一列火车由静止从车站出发，做匀加速直线运动，一观察者站在这列火车第一节车厢的前端，经过2s，第一节车厢全部通过观察者所在位置；全部车厢从他身边通过历时6s，设各节车厢长度相等，且不计车厢间距离。求：(1)这列火车共有多少节车厢?(2)最后2s内从他身边通过的车厢有多少车?(3)最后一节车厢通过观察者的时间是多少?

　 　　　　设t=0开始计时，V₀=0，s=0则：

1．等分运动时间(以T为时间单位)

　　 (1)lT末、2T末、3T末……瞬时速度之比为

　　　　 V_l：V₂：V₃……=1：2：3……

　　 (2)1T内、2T内、3T内……位移之比

　　　　 S_l：S₂：S₃……=1：4：9……

　　 (3)第一个T内、第二个T内、第三个T内……的位移之比为

　　　 S_Ⅰ：S_Ⅱ：S_Ⅲ…·=l：3：5……

9.　　　 看下图，此类题目重要的是画出示意图，会画图才会解题。

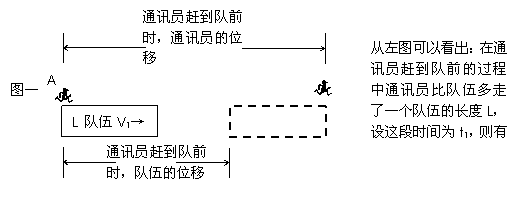
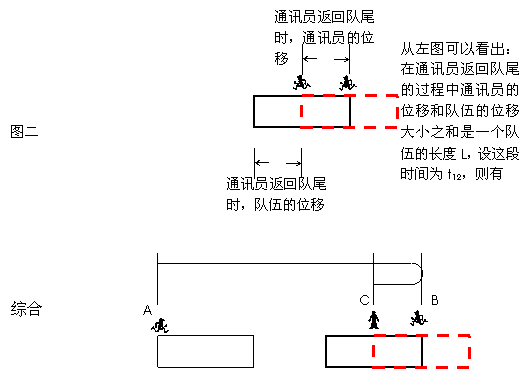
整个过程中队伍的位移是

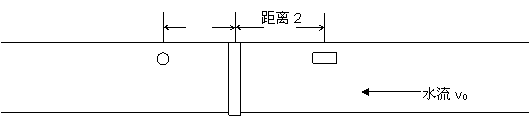
距离1是半小时内帽子以与水流相同的速度v₀向下游移动的距离

距离2是半小时内船以相对于河岸的速度v-v₀向上游的距离。

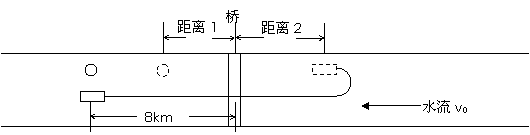
回头追赶帽子时，船相对于两岸的速度为v₀+v。

设从物体落水到发现物体落水的时间为，从发现落水到追到物体时间为，看图发现：为了追上物体，在时间内船必须比帽子多走距离1与距离2之和，则有：，总时间就有了：1h。所以水流速度为。

方法二、以流水为参考系，是物体相对于流水是静止的，而物体向上游的速度和追赶物体向下游的速度相对于流水速度是相同的，所以，如果选择流水为参考系，则整个过程是这样的：帽子掉下后静止不动，船向前走半小时后再回来取帽子还是需要半小时。不明白，类比生活中的乘列车：若列车以速度v₀向左运动，人的行走速度是v，当列车经过一个加油站时，你若不慎将帽子落在第一车厢，则可知落在地上的帽子相对于地面的速度是v₀，相对于车厢是静止的，你将帽子落在第一车厢后并没有发觉，而是继续在列车上向右行走，此时你相对于地面的速度是v-v₀，相对于车厢的速度是v，半小时后你发现了，要回来取帽子，你说要多长时间呢？(如果你半小时从第一车厢走到第五车厢，那么从第五车厢走到第一车厢要多长时间呢？)所以选择不同的参考系解题过程是不一样的。

8.　　　 解题时要学会把握已知量，有的条件是以文字形式告诉你的，那你要把它转变成可用于计算的量。如题中讲前一半时间或前一半位移，这全是文字表达的形式，我们要把它变成计算可用的量。前一半时间我们可以用(或t)，那一半时间也是(或t)，总时间就是t(或2t)；位移也是如此，则有下图

；

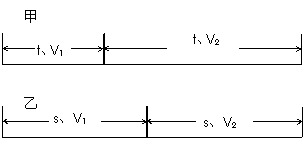
又因为

所以甲的时间比乙的时间少。

7.　　　 问题关键点在于数到21时其实只走过了20段根钢轨，了解这个后计算就很简单了

6.　　　 t=0时，物体距离O点5m，t=2s时物体距离O点21m，有

t=3s时物体距离O点59m，有