3．某学校有六个年级，人数分别为200、200、180、150、150、120，为加强学校民主化管理，拟就某项重大决策进行问卷调查，样本容量为100，下列做法符合统计学原理的是

A．午餐时间在食堂随意选定100人

B．先广播通知，然后在学生会门口将调查卷发给前100位来领取表格　　 的同学

C．把全校学生编码，用计算机随机抽取100人，发给调查卷

D．把调查卷分给各年级，数目如下：20、20、18、15、15、12．由各年级给本年级学生编码，用计算机随机抽取相应数目，发给问卷

2.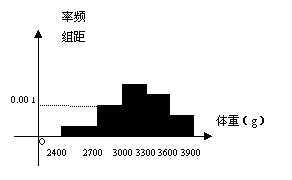 4．观察新生婴儿的体重，其频率分布直方图如右下图所示，则新生婴儿的体重在(　　 ).

A. 　0．001　B．0．3　 C．0．01　D．0．003

[基础自测]

1．一个容量为20的样本，数据的分组几个组的频数如下：

则样本在区间上的频率为(　)．

A．0．5　　B．0．7　C．0．25　D．0．05

4.袋中装着标有数学1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用表示取出的3个小球上的最大数字，求：(1)取出的3个小球上的数字互不相同的概率；

(2)随机变量的概率分布和数学期望；

(3)计分介于20分到40分之间的概率．

3、9粒种子分种在3个坑内，每坑3粒，每粒种子发芽的概率为0　 5，若一个坑内至少有1粒种子发芽，则这个坑不需要补种，若一个坑内的种子都没发芽，则这个坑需补种假定每个坑至多补种一次，每补种1个坑需10元，用ξ表示补种费用，写出ξ的分布列并求ξ的数学期望　 (精确到0　 01)

2．[05湖北]某地最近出台一项机动车驾照考试规定；每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止.如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数的分布列和的期望,并求李明在一年内领到驾照的概率.

1． 设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯(允许通行)的概率为，遇到红灯(禁止通行)的概率为。假定汽车只在遇到红灯或到达目的地才停止前进，表示停车时已经通过的路口数，求：

(1)的概率的分布列及期望E;

　(2 )　 停车时最多已通过3个路口的概率.

10．设是离散性随机变量，

的值为(　)．

A．　B．　C．3　D．

[典例分析]

例1　从10位同学(其中6女，4男)中随机选出3位参加测验.每位女同学能通过测验的概率均为，每位男同学能通过测验的概率均为.试求：

(1)选出的3位同学中，至少有一位男同学的概率；

(2)10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.

例2袋子A和B中装有若干个均匀的红球和白球，从A中摸出一个红球的概率是，从B中摸出一个红球的概率为p．

　 (Ⅰ) 从A中有放回地摸球，每次摸出一个，有3次摸到红球即停止．

(i)求恰好摸5次停止的概率；

(ii)记5次之内(含5次)摸到红球的次数为，求随机变量的分布率及数学期望E．

　 (Ⅱ) 若A、B两个袋子中的球数之比为1:2，将A、B中的球装在一起后，从中摸出一个红球的概率是，求p的值．

例3[07全国2]从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件：“取出的2件产品中至多有1件是二等品”的概率．

(1)求从该批产品中任取1件是二等品的概率；

(2)若该批产品共100件，从中任意抽取2件，表示取出的2件产品中二等品的件数，求的分布列．

例4..[06天津]某射手进行射击训练,假设每次射击击中目标的概率为,且各次射击的结果互不影响.

(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答)；

(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答)；

(3)设随机变量表示射手第3次击中目标时已射击的次数,求的分布列．

[巩固练习]

9．已知某离散性随机变量的数学期望E，的分布列如下：

	0	1	2	3
P	a			b

则a= 　　　　.

8．已知的分布列为：且设

A．　　B．　C．1　　D．