有一个选项符合题意，选对的得3分，有选错或不选的得0分。)

1．一汽车在路面情况相同的公路上直线行驶，下面关于车速、惯性、质量和滑行路程的讨论，正确的是　　　　　　　　 　 (　　 )

　　　 A．车速越大，它的惯性越大　　

　　　 B．质量越大，它的惯性越大

　　　 C．质量越大，刹车后滑行的路程越长

　　　 D．车速越大，刹车后滑行的路程越长，所以惯性越大

21．(本小题满分14分)

已知函数(x∈R)在区间[-1,1]上是增函数．

(Ⅰ)求实数a的值所组成的集合A；

(Ⅱ)设关于x的方程的两实数根为x₁、x₂,试问:是否存在实数m,使得不等式对任意a∈A及t∈[-1,1]恒成立?若存在,求0出m的取值范围;若不存在,请说明理由?

20．(本小题满分14分)

已知两点M(-1,0), N(1, 0), 且点P使成公差小于零的等差数列．

(Ⅰ)求点P的轨迹方程方程；

(Ⅱ)若点P的坐标为(x_0, y₀), 记θ为,的夹角, 求

19．(本小题满分13分)

某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇．

(I)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇，试确定小艇航行速度的最小值．

18．(本小题满分13分)

若＝，＝,其中>0,记函数f(x)=(+)·+k．

(1)若f(x)图象中相邻两条对称轴间的距离不小于，求的取值范围．

(2)若f(x)的最小正周期为，且当x时，f(x)的最大值是，求f(x)的解析式，

17．(本小题满分13分)

已知实数有极大值32．

(1)求函数的单调区间；　

(2)求实数的值．

16．(本小题满分13分)

已知均为等差数列，且，求数列的前100项之和。

15．定义“等积数列”：在一个数列中，如果每一项与它的后一项的积都为同一个常数，那么这个数列叫做等积数列，这个常数叫做数列的公积。已知数列是等积数列，且，公积为8，那么的值为　　　　　　　　　　 　，这个数列的前

14．8．已知向量，直线l过点，且与向量垂直，则直线l的一般方程是　　　　　　　　　　　 　。

13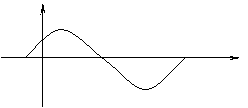．函数f(x)=A sin (w x+ j )

　 (A>0, w >0, | j |< )的一段

图象过点，如图所示．

则函数f (x)的解析式　　　　 。