18.(14分) 对某人某二项指标进行考核，每项指标满分100分,设此人每项得分在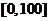上是等可能出现的.单项80分以上，且总分170分以上才合格，求他合格的概率。

17.(16分) 将完全相同的3个球随机地放入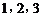号盒子中(每盒放球数不限)，求：

(1)3个球放入同一个盒子的概率；(2)3个盒子中都有球的概率；(3)至少有一个盒子没球的概率；(4)恰有一个盒子没有球的概率.

16.(14分) 到银行办理个人异地汇款(不超过100万元)，银行收取一定的手续费，汇款额不超过100元，收取1元手续费，超过100元但不超过5 000元，按汇款额的1%收取，超过5 000元，一律收取50元手续费，请用条件语句描述汇款额为x元时，银行收取手续费y元的过程，并画出流程图.

15．(14分) 假设关于某设备的使用年限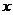和所支出的维修费用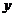(万元)，有如下的统计资料：

若由资料知y与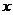呈线性相关关系．求：

(1)线性回归方程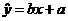的回归系数；

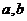(2)估计使用年限为10年时，维修费用是多少？

14.有一个公用电话亭，在观察使用这个电话的人的流量时，设在某一时刻有n个人正在使用电话或等待使用的概率为P(n)，且P(n)与时刻t无关，统计得到

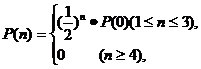那么在某一时刻，这个公用电话亭里一个人也没有的概率是　　 ▲　　 ．

13.考虑一元二次方程x²+mx+n=0，其中m、n的取值分别等于将一枚骰子连掷两次先后出现的点数，则方程有实根的概率为　　 ▲　　 ．　　　　　　　

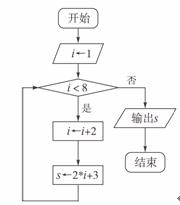
12.如右图给出的算法流程图中，输出的结果s=　　 ▲　　 ．

11．一块各面均有油漆的正方体被锯成1000个同样大小的正方体，若将这些小正方体均匀搅混在一起，则任意取出的一小正方体其两面均涂有油漆的概率是　　 ▲　　 ．

10. 若随机向一个边长为2的正三角形内丢一粒豆子， 则豆子落在此三角形内切圆内的概率是　　 ▲　　 ．

9.已知样本数据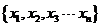的平均数为h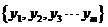，的平均数为k, 则把两组数据合并成一组以后，这组样本数据的平均数为　　 ▲　　 ．