
5、下列有关文学常识的表述,错误的一项是( )
A、《左传》是我国第一部叙事详细的编年体史书,作者相传是左丘明;《史记》是我国第一部纪传体通史,作者是西汉的司马迁。
B、儒家经典《论语》和“半自传体”小说《大卫·科波菲尔》分别是我国春秋末期孔子和英国作家查尔斯·狄更斯的作品。
C、词是诗歌的一种,最初是配合音乐来歌唱的,根据字数多少,可分为小令、中调、长调。由于词的句子长短不一,所以也称为“长短句”
D、中外名著常有一个精妙的开头语,例如俄国作家列夫·托尔斯泰的《安娜·卡列尼娜》中的“幸福的家庭都是相似的,不幸的家庭各有各的不幸”,中国作家罗贯中的《三国演义》中的“话说天下大势,分久必合,合久必分”。
4、下列各句中,没有语病的一句是( )
A、青藏铁路纵贯青海、西藏两省区,跨越青藏高原,是连接西藏与内地的一条具有重要战略意义的铁路干线。
B、天安门广场等七个红色旅游景点是否收门票的问题,国家旅游局新闻发言人已在记者招待会上予以否认。
C、不少学生偏食、挑食,导致蛋白质的摄入偏低,钙、锌、铁等营养素明显不足,营养状况不容令人乐观。
D、这家乒乓球馆设施齐全,可为乒乓球爱好者提供不同档次的球台、球拍、球衣、球鞋等乒乓球器材。
3、下列各句中加点的成语使用恰当的一句是( )
A、许多农民巧妙地将服装厂剪裁后废弃的“下脚料”做成帘子,当作蔬菜大棚的“棉被”,这真是一念之差,变废为宝。
B、2006年夏天,我国大部分地区出现了罕见的高温天气,七月流火的酷暑使一些地区电力供应紧张。
C、为了不使中华民族处于“人为刀俎,我为鱼肉”的危险境地,我们只有奋起反抗,把侵略者赶出国土。
D、厂长动情地说:“为了扭转目前的不利局面,我们将采用一种新的对策,希望大家共同努力,功败垂成,在此一举!”
2、下列词语中书写完全正确的一组是( )
A、廖廓 张驰 篱笆 执拗
B、浪谒飞舟 尸骸 屠戳 作揖
C、笙箫 攒射 撰写 窒息
D、荡漾 菲闻 婆娑 荤腥
1、下列词语中加点的字注音不完全正确的一组是( )
A、百舸(gě) 峥嵘(zhēng róng) 颓圮(pǐ) 殒身不恤(xù)
B、寥落(liáo) 荆棘(jīng jí) 浸渍( zì) 长歌当哭(dàng)
C、揩油(kāi) 菲薄(fěi bó) 洗涤( dí ) 挥斥方遒(qiú)
D、封侯(hòu) 论语(lún) 谄媚(xiàn) 忸怩不安(niŭ ní)
空间两点间的距离公式及其与平面两点间距离公式的联系和区别
教学设计方案
第 四 单元 第 9 课 年 月 日
|
课题 |
本章复习 |
|
|
三 维 教 学 目 标 |
知识与 能力 |
(1)熟悉圆的方程及判断直线与圆的位置的方法(ABC) (2)会用待定系数法求圆的方程(ABC) (3)会解决对称性的问题(AB) |
|
过程与 方法 |
进一步培养学生能用解析法研究几何问题的能力,渗透数形结合思想,通过圆的标准方程解决实际问题的学习,注意培养学生观察问题、发现问题和解决问题的能力。 |
|
|
情感、 态度、 价值观 |
通过运用圆的知识解决实际问题的学习,从而激发学生学习 数学的热情和兴趣. |
|
|
教 学 内 容 分 析 |
教学 重点 |
会用待定系数法求圆的方程 |
|
教学 难点 |
会用待定系数法求圆的方程 |
|
|
教学过程 |
||
|
一、知识结构 1、圆的方程:标准方程和一般方程 2、直线与圆、圆与圆的位置关系 3、直线与圆的方程的简单应用:坐标法 二、讲授新课 1、求下列圆的方程(ABC) (1)圆心为点M(-5,3),且过点A(-8,-1) (2)过三点A(-2,4)、B(-1,3)、C( 2,6 ) 2、已知圆x2+y2=4和圆x2+y2+4x-4y+4=0关于直线 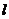 对称,求直线 对称,求直线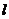 的方程 的方程分析:直线 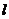 是圆心连线的垂直平分线(ABC) 是圆心连线的垂直平分线(ABC)变式练习 求与圆(x+2)2+(y-6)2=1关于直线3x-4y+5=0对称的圆的方程(AB) 分析:关键求出圆心,已知半径为1,利用直线是圆心连线的垂直平分线。 三、小结 解决对称问题的方法 |
||
|
课 后 学 习 |
复习参考题A组5、8 |
|
|
教 学 反 思 |
学生对圆的方程有关知识掌握不好,本节对这部分知识进行梳理,帮助学生形成知识结构,加深理解,巩固知识,效果较好。 |
教学设计方案
第 四 单元 第 10 课 年 月 日
|
课题 |
本章复习 |
|
|
三 维 教 学 目 标 |
知识与 能力 |
(1)
熟悉直线方程的五种形式(ABC) (2) 会求直线方程(ABC) (3)会判断直线的位置关系(AB) |
|
过程与 方法 |
2.判断两直线位置的方法。 2.掌握数形结合的学习法。 |
|
|
情感、 态度、 价值观 |
1.通过直线方程和二元一次方程的联系,从而认识事物之间的内的联系。 2.能够用辩证的观点看问题。 |
|
|
教 学 内 容 分 析 |
教学 重点 |
求直线方程,判断直线的位置关系 |
|
教学 难点 |
判断直线的位置关系 |
|
|
教学过程 |
||
|
一、知识结构 1、直线方程的形式 2、判断直线的位置关系 3、两点间距离、点到直线的距离、两条平行线的距离 二、新课 (一)基础练习(ABC) 1、经过两点A(4 , 2m+1),B(2,-3)的直线倾斜角为1350,则m的值为( ) A、- 1 B、 -3 C、 1 D、2 2、菱形ABCD的相对顶点A(1,-2)、C(-2,-3),则对角线BD所在直线的方程是( ) A 、3x+y+4=0 B、3x+y-4=0 C、 3x-y+1=0 D、3x-y-1=0 3、若直线  互相垂直,则a的值为( )A o或 互相垂直,则a的值为( )A o或 B 1 C 1或-3 D -3 B 1 C 1或-3 D -3(二)典型例题 1、求过点(1,-4)且与直线2x+3y+5=0平行的直线方程(ABC) 求过两直线3x-2y+1=0和x+3y+4=0的交点,且垂直于直线x+3y+4=0的直线方程 2、已知A(1,2)、B(3,4)、C(5,0),求△ABC的面积(AB C) 3、正方形的中心在(-1,0),一条所在直线方程为x+3y-5=0,求其他三条边所在的直线方程(AB) 三、小结 与Ax+By+C=0平行的直线方程可设为Ax+By+m=0 垂直的直线方程可设为Bx-Ay+n=0 |
||
|
课 后 学 习 |
复习参考题A组11、12 |
|
|
教 学 反 思 |
梳理知识点,形成知识结构,在此基础上适当做练习巩固知识,再设计层次高点的练习,进行提升。 |
4、课本P150练习4(AB)
3、课本P150练习1、2、3(ABC)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com