
26、 ,其中
,其中 .
.
25、二倍角的正弦、余弦和正切公式:
⑴ .
.
⑵ (
(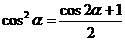 ,
, ).
).
⑶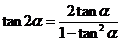 .
.
24、两角和与差的正弦、余弦和正切公式:
⑴ ;
;
⑵ ;
;
⑶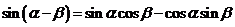 ;
;
⑷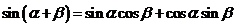 ;
;
⑸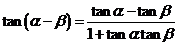 (
( );
);
⑹ (
(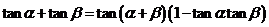 ).
).
23、平面向量的数量积:
⑴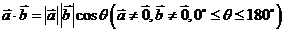 .零向量与任一向量的数量积为
.零向量与任一向量的数量积为 .
.
⑵性质:设 和
和 都是非零向量,则①
都是非零向量,则① .②当
.②当 与
与 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;
; 或
或 .③
.③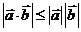 .
.
⑶运算律:① ;②
;② ;③
;③ .
.
⑷坐标运算:设两个非零向量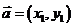 ,
, ,则
,则 .
.
若 ,则
,则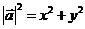 ,或
,或 .
.
设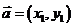 ,
, ,则
,则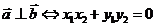 .
.
设 、
、 都是非零向量,
都是非零向量,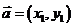 ,
, ,
,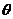 是
是 与
与 的夹角,则
的夹角,则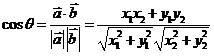 .
.
22、分点坐标公式:设点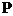 是线段
是线段 上的一点,
上的一点, 、
、 的坐标分别是
的坐标分别是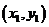 ,
, ,当
,当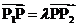 时,点
时,点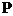 的坐标是
的坐标是 .
.
21、平面向量基本定理:如果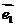 、
、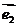 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量 ,有且只有一对实数
,有且只有一对实数 、
、 ,使
,使 .(不共线的向量
.(不共线的向量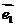 、
、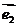 作为这一平面内所有向量的一组基底)
作为这一平面内所有向量的一组基底)
20、向量共线定理:向量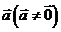 与
与 共线,当且仅当有唯一一个实数
共线,当且仅当有唯一一个实数 ,使
,使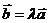 .
.
设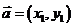 ,
, ,其中
,其中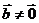 ,则当且仅当
,则当且仅当 时,向量
时,向量 、
、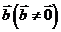 共线.
共线.
19、向量数乘运算:
⑴实数 与向量
与向量 的积是一个向量的运算叫做向量的数乘,记作
的积是一个向量的运算叫做向量的数乘,记作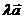 .
.
①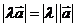 ;
;
②当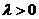 时,
时,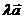 的方向与
的方向与 的方向相同;当
的方向相同;当 时,
时,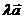 的方向与
的方向与 的方向相反;当
的方向相反;当 时,
时, .
.
⑵运算律:①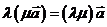 ;②
;②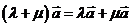 ;③
;③ .
.
⑶坐标运算:设 ,则
,则 .
.
18、向量减法运算:
⑴三角形法则的特点:共起点,连终点,方向指向被减向量.
⑵坐标运算:设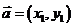 ,
, ,则
,则 .
.
设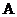 、
、 两点的坐标分别为
两点的坐标分别为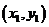 ,
, ,则
,则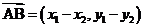 .
.
17、向量加法运算:
⑴三角形法则的特点:首尾相连.
⑵平行四边形法则的特点:共起点.
⑶三角形不等式: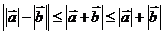 .
.
 ⑷运算性质:①交换律:
⑷运算性质:①交换律: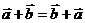 ;②结合律:
;②结合律: ;③
;③ .
.
⑸坐标运算:设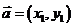 ,
, ,则
,则 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com