
20.(本题满分14分)
设 比较
比较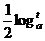 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
解:
19.(本题满分12分).
如图,有一个圆柱形的无盖杯子,它的内表面积是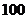
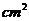 ,
,
 试用解析式将杯子的容积
试用解析式将杯子的容积 (
( )表示成底面内半径
)表示成底面内半径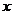 (
( )的函数.
)的函数.
分析:圆柱形的无盖杯子,内表面积=底面积+侧面积
解:
17、若函数 分别是
分别是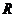 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足 ,则有( )
,则有( )
A.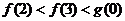 B.
B.
C. D.
D.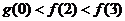
18若定义在R上的函数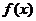 满足:对任意
满足:对任意 有
有 ,则下列说法一定正确的是( )
,则下列说法一定正确的是( )
(A)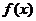 为奇函数 (B)
为奇函数 (B)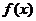 为偶函数
为偶函数
(C)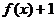 为奇函数 (D)
为奇函数 (D)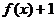 为偶函数
为偶函数
16、函数 的图像关于(
)
的图像关于(
)
A. 轴对称
B.直线
轴对称
B.直线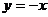 对称
对称
C.坐标原点对称 D.直线 对称
对称
15、若非空集合 满足
满足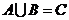 ,且
,且 不是
不是 的子集,则( )
的子集,则( )
A.“ ”是“
”是“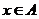 ”的充分条件但不是必要条件
”的充分条件但不是必要条件
B.“ ”是“
”是“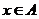 ”的必要条件但不是充分条件
”的必要条件但不是充分条件
C.“ ”是“
”是“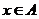 ”的充要条件
”的充要条件
D.“ ”既不是“
”既不是“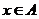 ”的充分条件也不是“
”的充分条件也不是“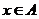 ”必要条件
”必要条件
14、已知函数 ,若
,若 ,且
,且 ,则
,则 的取值范围是______
的取值范围是______
13、非空集合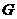 关于运算
关于运算 满足:(1)对任意
满足:(1)对任意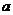 、
、 ,都有
,都有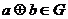 ;(2)存在
;(2)存在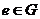 ,使得对一切
,使得对一切 ,都有
,都有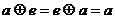 ,则称
,则称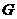 关于运算
关于运算 为“融洽集”.现给出下列集合和运算:
为“融洽集”.现给出下列集合和运算:
①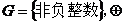 为整数的加法.②
为整数的加法.②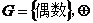 为整数的乘法.
为整数的乘法.
③ 为平面向量的加法.④
为平面向量的加法.④ 为多项式的加法.
为多项式的加法.
⑤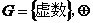 为复数的乘法.其中
为复数的乘法.其中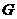 关于运算
关于运算 为“融洽集”的是____________(写出所有“融洽集”的序号)
为“融洽集”的是____________(写出所有“融洽集”的序号)
12、定义在 上的函数
上的函数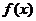 满足
满足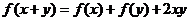 (
(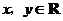 ),
), ,则
,则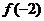 等于__________
等于__________
11、若函数 的图像与函数
的图像与函数 的图像关于直线
的图像关于直线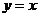 对称,则
对称,则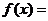 ____________
____________
10、设奇函数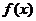 在
在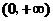 上为增函数,且
上为增函数,且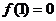 ,则不等式
,则不等式 的解集为___________________
的解集为___________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com