
22.(本小题满分15分)
已知抛物线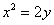 的焦点为F,准线为
的焦点为F,准线为 ,过
,过 上一点P,作抛物线的两条切线,
上一点P,作抛物线的两条切线,
切点分别为A、B,某数学兴趣小组在研究讨论中,提出如下两个猜想:
① 直线PA、PB垂直;
② 等式 中
中 为常数;
为常数;
现请你进行一一验证这两个猜想是否成立。
21. (本题满分15分)
已知函数 的图象为曲线C。
的图象为曲线C。
(1)若曲线C上存在点P,使曲线C在P点处的切线与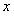 轴平行,求
轴平行,求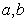 的关系;
的关系;
(2)若函数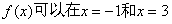 时取得极值,求此时
时取得极值,求此时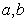 的值;
的值;
(3)在满足(2)的条件下,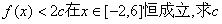 的取值范围。
的取值范围。
20. (本小题满分14分)已知数列 是首项为
是首项为 ,公比
,公比 的等比数列,
的等比数列,
设 ,数列
,数列 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列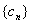 的前n项和
的前n项和 .
.
19. (本小题满分14分)
如图,已知四棱锥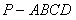 中,
中,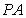 ⊥平面
⊥平面 ,
,
 是直角梯形,
是直角梯形, ,
,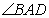
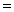 90º,
90º, .
.
(1)求证: ⊥
⊥ ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使
,使 //平面
//平面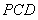 ,
,
若存在,指出点 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.

18、(本小题满分14分)
已知
(1)求函数 的最小正周期;
的最小正周期;
(2)当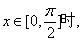 求函数
求函数 的最大值及最小值。
的最大值及最小值。
17、已知函数 ,
,
则 = ▲ .
= ▲ .
16、
对于大于1的自然数 的
的 次幂可用奇数进行如图所示的“分裂”,仿此,记
次幂可用奇数进行如图所示的“分裂”,仿此,记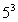 的“分裂”中的最小数为
的“分裂”中的最小数为 ,而
,而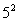 的“分裂”中最大的数是
的“分裂”中最大的数是 ,则
,则 ▲ .
▲ .
15、若 且
且

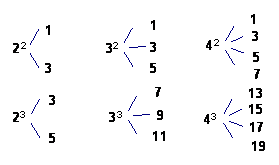 则
则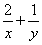 的最小值是
▲ .
的最小值是
▲ .
14、在腰长为2的等腰直角三角形内任取一点,使得该点到此三

角形的直角顶点的距离不大于1的概率为 ▲ .
13、如图所示的算法流程图中,输出S的值为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com