4.四个函数:①f(x)=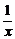;②g(x)=sinx;③f(x)=|x|;④f(x)=ax³+bx²+cx+d.其中在x=0处连续的函数是____________.(把你认为正确的代号都填上)

答案：②③④

●典例剖析

[例1] (1)讨论函数f(x)=

(2)讨论函数f(x)=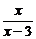在区间［0,3］上的连续性.

剖析：(1)需判断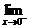f(x)=f(x)=f(0).

(2)需判断f(x)在(0,3)上的连续性及在x=0处右连续,在x=3处左连续.

解:(1)∵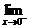f(x)=－1, f(x)=1,

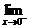f(x)≠f(x),

∴f(x)不存在.∴f(x)在x=0处不连续.

(2)∵f(x)在x=3处无定义,

∴f(x)在x=3处不连续.

∴f(x)在区间［0,3］上不连续.

[例2] 设f(x)=当a为何值时,函数f(x)是连续的.

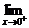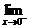解:f(x)= (a+x)=a, f(x)=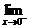e^x=1,而f(0)=a,故当a=1时, 　　　f(x)=f(0),

即说明函数f(x)在x=0处连续,而在x≠0时,f(x)显然连续,于是我们可判断当a=1时,

f(x)在(－∞,+∞)内是连续的.

评述：分段函数讨论连续性,一定要讨论在“分界点”的左、右极限,进而断定连续性.

[例3] 如右图,在大沙漠上进行勘测工作时,先选定一点作为坐标原点,然后采用如下方法进行:从原点出发,在x轴上向正方向前进a(a＞0)个单位后,向左转90°,前进a r(0＜r＜1＝个单位,再向左转90°,又前进a r²个单位,…,如此连续下去.

(1)若有一小分队出发后与设在原点处的大本营失去联系,且可以断定此小分队的行动与原定方案相同,则大本营在何处寻找小分队?

(2)若其中的r为变量,且0＜r＜1,则行动的最终目的地在怎样的一条曲线上?

剖析：(1)小分队按原方案走,小分队最终应在运动的极限位置.

(2)可先求最终目的地关于r的参数形式的方程.

解:(1)由已知可知即求这样运动的极限点,设运动的极限位置为Q(x,y),则

x=a－ar²+ar⁴－…==,

y=ar－ar³+ar⁵－…=,

∴大本营应在点(,)附近去寻找小分队.

(2)由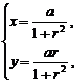消去r得(x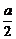－)²+y²=(其中x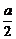＞,y＞0),

即行动的最终目的地在以(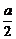,0)为圆心,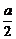为半径的圆上.

●闯关训练

夯实基础

3.下列图象表示的函数在x=x₀处连续的是

A.①　　　 　　　　B.②③　　　　　　 C.①④　　　　　　　 D.③④

答案：A

2.f(x)=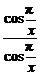的不连续点为

A.x=0

B.x=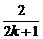(k=0,±1,±2,…)

C.x=0和x=2kπ(k=0,±1,±2,…)

D.x=0和x=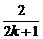(k=0,±1,±2,…)

解析：由cos=0,得=kπ+(k∈Z),∴x=.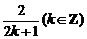

又x=0也不是连续点,故选D

答案：D

1.f(x)在x=x₀处连续是f(x)在x=x₀处有定义的_________条件.

A.充分不必要　　　　　　　　　　　　　　　 B.必要不充分

C.充要　　　　　　　　　　　　　　　　　　 D.既不充分又不必要

解析：f(x)在x=x₀处有定义不一定连续.

答案：A

3.若f(x)、g(x)都在点x₀处连续,则f(x)±g(x),f(x)·g(x),(g(x)≠0)也在点x₀处连续.若u(x)在点x₀处连续,且f(u)在u₀=u(x₀)处连续,则复合函数f［u(x)］在点x₀处也连续.

特别提示

　(1)连续必有极限,有极限未必连续.

(2)从运算的角度来分析,连续函数在某一点处的极限运算与函数关系“f”是可以交换顺序的.

●点击双基

2.如果f(x)是闭区间［a,b］上的连续函数，那么f(x)在闭区间［a,b］上有最大值和最小值.

1.函数的连续性.

一般地，函数f(x)在点x=x₀处连续必须满足下面三个条件：

(1)函数f(x)在点x=x₀处有定义；(2)f(x)存在；(3)f(x)=f(x₀).如果函数y=f(x)在点x=x₀处及其附近有定义，而且f(x)=f(x₀),就说函数f(x)在点x₀处连续.

13.4　 函数的连续性及极限的应用

●知识梳理

2.应用导数解决实际问题，关键是要建立恰当的数学模型(函数关系)，如果函数在区间内只有一个点使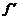(x)=0，此时函数在这点有极大(小)值，那么不与端点比较，也可以知道这就是最大(小)值.

拓展题例

[例1] 函数y=2x³+3x²－12x+14在［－3，4］上的最大值为________，最小值为________.

解析：y′=6x²+6x－12=0.

x=1，－2，f(－3)=20，f(－2)=34，f(1)=7，f(4)=142.

答案：142　 7

[例2] 设x=－2与x=4是函数f(x)=x³+ax²+bx的两个极值点.

(1)求常数a、b；

(2)判断x=－2，x=4是函数f(x)的极大值点还是极小值点，并说明理由.

解：(1)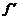(x)=3x²+2ax+b.

由极值点的必要条件可知x=－2和x=4是方程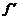(x)=0的两根，则a=－3，b=－24.

(2)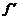(x)=3(x+2)(x－4)，得

当x<－2时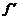，(x)>0；

当－2<x<4时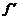，(x)<0.

∴x=－2是f(x)的极大值点.

当x>4时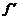，(x)>0，则x=4是f(x)的极小值点.

1.导数的基本应用如下表：