2.设函数f(x)在x=x₀处可导,则

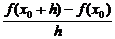
A.与x₀,h都有关

B.仅与x₀有关而与h无关

C.仅与h有关而与x₀无关

D.与x₀、h均无关

答案:B

1.在曲线y=x²+1的图象上取一点(1,2)及邻近一点(1+Δx,2+Δy),则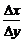为

A.Δx+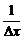+2　 　　　　　　　　　　　　　B.Δx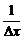－－2

C.Δx+2　　　　　　　　　　　　　　　　 D.2+Δx－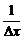

解析: 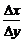==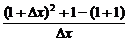Δx+2.

答案:C

4.导数的四则运算法则：

设u、v是可导函数，则

(u±v)′=u′±v′;(uv)′=u′v+uv′;(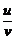)′= (v≠0).

特别提示

f(x)在x=x₀处的导数f′(x₀)的实质是“增量之比的极限”，但在计算中取它的应用含义：f′(x₀)是函数f(x)的导函数f′(x)当x=x₀时的函数值.

●点击双基

3.几种常见的导数：

C′=0(C为常数);(xⁿ)′=nx^n－1;(sinx)′=cosx;(cosx)′=－sinx;(e^x)′=e^x;　　　　　 (a^x)′=a^xlna;(lnx)′=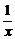;(log_ax)′=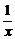log_ae.

2.导数的几何意义：函数y=f(x)在点x₀处的导数的几何意义，就是曲线y=f(x)在点P(x₀,f(x₀))处的切线的斜率.

1.导数的概念：(1)如果当Δx→0时，有极限，我们就说函数y=f(x)在点x₀处可导，并把这个极限叫做f(x)在点x₀处的导数，记作f′(x₀)，即f′(x₀)=　　　　　　　　　　　　 　=.

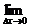
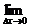
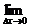
(2)如果函数f(x)在开区间(a,b)内每一点都可导，就说f(x)在开区间(a,b)内可导.这时对于开区间(a,b)内每一个确定的值x₀,都对应着一个确定的导数f′(x₀),这样就在开区间(a,b)内构成一个新的函数，这一新函数叫做f(x)在开区间(a,b)内的导函数，记作f′(x),即f′(x)= 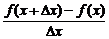，导函数也简称导数.

14.1　 导数的概念与运算

●知识梳理

2.掌握导数运算在判断函数的单调性、求函数的极大(小)值中的应用,尤其要重视导数运算在解决实际问题中的最值问题时所起的作用.

1.熟练记忆基本求导公式和函数的求导法则,是正确进行导数运算的基础.

2.函数f(x)在点x₀处连续必须具备以下三个条件:

函数f(x)在点x=x₀处有定义;

函数f(x)在点x=x₀处有极限;

函数f(x)在点x=x₀处的极限值等于在这一点x₀处的函数值,即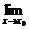f(x)=f(x₀).

这三个条件缺一不可,是我们判断函数在一点处是否连续的重要工具.

●拓展题例

[例题] 一弹性小球自h₀=5 m高处自由下落,当它与水平地面每碰撞一次后速度减少到碰前的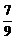,不计每次碰撞时间,计算小球从开始下落到停止运动所经过的路程和时间.

解：设小球第一次落地时速度为v₀,则有v₀=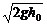=10(m/s),那么第二,第三,…,第n+1次落地速度分别为v₁=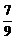v₀,v₂=(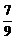)²v₀,…,v_n=(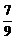)ⁿv₀,小球开始下落到第一次与地相碰经过的路程为h₀=5 m,小球第一次与地相碰到第二次与地相碰经过的路程是L₁=2×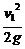=10×(.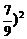

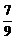小球第二次与地相碰到第三次与地相碰经过的路程为L₂,则L₂=2×=10×()⁴.

由数学归纳法可知,小球第n次到第n+1次与地面碰撞经过路程为L_n=10×(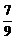)²ⁿ.

故从第一次到第n+1次所经过的路程为

S_n+1=h₀+L₁+L₂+…+L_n,则整个过程总路程为

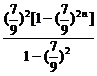S=S_n+1=5+10×=5+10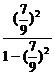=20.3(m),小球从开始下落到第一次与地面相碰经过时间t₀=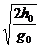=1(s).

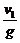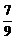小球从第一次与地相碰到第二次与地相碰经过的时间t₁=2×=2×,同理可得

t_n=2×(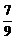)ⁿ,t_n+1=t₀+t₁+t₂+…+t_n,则t=t_n+1=1+2×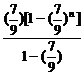=8(s).

上例是借助数学工具来解决物理问题,这样有利于学生对数学知识的进一步理解,增强学生对数学的应用意识,培养学生的数学应用能力.