
4.集合问题多与函数、方程、不等式有关,要注意各类知识的融会贯通.解决问题时常用数形结合、分类讨论等数学思想.
●教师下载中心
教学点睛
3.含参数的集合问题,多根据集合元素的互异性来处理.
2.关于集合的运算,一般应把各参与运算的集合化到最简,再进行运算.
1.对于集合问题,要首先确定属于哪类集合(数集、点集或某类图形),然后确定处理此类问题的方法.
9.若B={x|x2-3x+2<0},是否存在实数a,使A={x|x2-(a+a2)x+a3<0}且A∩B=A?请说明你的理由.
解:∵B={x|1<x<2},若存在实数a,使A∩B=A,则A={x|(x-a)(x-a2)<0}.
(1)若a=a2,即a=0或a=1时,此时A={x|(x-a)2<0}=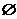 ,满足A∩B=A,∴a=0或a=1.
,满足A∩B=A,∴a=0或a=1.
(2)若a2>a,即a>1或a<0时,A={x|0<x<a2},要使A∩B=A,则
 1≤
1≤
a≤ ,∴1<a≤
,∴1<a≤ .
.
(3)若a2<a,即0<a<1时,A={x|a<x<a2},要使A∩B=A,则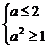
 1≤a≤2,∴a∈
1≤a≤2,∴a∈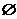 .
.
综上所述,当1≤a≤ 或a=0时满足A∩B=A,即存在实数a,使A={x|x2-(a+a2)x+
或a=0时满足A∩B=A,即存在实数a,使A={x|x2-(a+a2)x+
a3<0}且A∩B=A成立.
●思悟小结
8.已知P={(x,y)|(x+2)2+(y-3)2≤4},Q={(x,y)|(x+1)2+(y-m)2< },且P∩Q=Q,求m的取值范围.
},且P∩Q=Q,求m的取值范围.
解:点集P表示平面上以O1(-2,3)为圆心,2为半径的圆所围成的区域(包括圆周);点集Q表示平面上以O2(-1,m)为圆心, 为半径的圆的内部.要使P∩Q=Q,应使⊙O2内含或内切于⊙O1.故有|O1O2|2≤(R1-R2)2,即(-1+2)2+(m-3)2≤(2-
为半径的圆的内部.要使P∩Q=Q,应使⊙O2内含或内切于⊙O1.故有|O1O2|2≤(R1-R2)2,即(-1+2)2+(m-3)2≤(2- )2.解得3-
)2.解得3-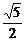 ≤m≤3+
≤m≤3+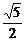 .
.
评述:本题选题目的是:熟悉用集合语言表述几何问题,利用数形结合方法解题.
探究创新
7.已知A={x∈R|x2+2x+p=0}且A∩{x∈R|x>0}=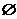 ,求实数p的取值范围.
,求实数p的取值范围.
解:∵A∩{x∈R|x>0}=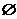 ,
,
∴(1)若A=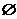 ,则Δ=4-4p<0,得p>1;
,则Δ=4-4p<0,得p>1;
(2)若A≠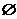 ,则A={x|x≤0},
,则A={x|x≤0},
即方程x2+2x+p=0的根都小于或等于0.
设两根为x1、x2,则
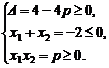 ∴0≤p≤1.
∴0≤p≤1.
综上所述,p≥0.
6.(2005年春季北京,15)记函数f(x)=log2(2x-3)的定义域为集合M,函数g(x)=  的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M、N;
(2)集合M∩N、M∪N.
解:(1)M={x|2x-3>0}={x|x>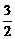 };
};
N={x|(x-3)(x-1)≥0}={x|x≥3或x≤1}.
(2)M∩N={x|x≥3};
M∪N={x|x≤1或x>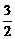 }.
}.
培养能力
5.(2004年全国Ⅰ,理6)设A、B、I均为非空集合,且满足A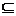 B
B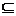 I,则下列各式中错误的是
I,则下列各式中错误的是
A.(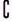 IA)∪B=I B.(
IA)∪B=I B.(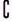 IA)∪(
IA)∪(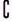 IB)=I
IB)=I
C.A∩(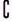 IB)=
IB)=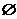 D.(
D.(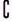 IA)∩(
IA)∩(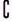 IB)=
IB)=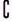 IB
IB
解析一:∵A、B、I满足A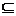 B
B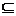 I,先画出文氏图,根据文氏图可判断出A、C、D都是正确的.
I,先画出文氏图,根据文氏图可判断出A、C、D都是正确的.

解析二:设非空集合A、B、I分别为A={1},B={1,2},I={1,2,3}且满足A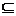 B
B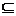 I.根据设出的三个特殊的集合A、B、I可判断出A、C、D都是正确的.
I.根据设出的三个特殊的集合A、B、I可判断出A、C、D都是正确的.
答案:B
4.已知集合A={x∈R|ax2+2x+1=0,a∈R}只有一个元素,则a的值为__________________.
解析:若a=0,则x=- .
.
若a≠0,Δ=4-4a=0,得a=1.
答案:a=0或a=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com