
1.有的“p或q”与“p且q”形式的复合命题语句中,字面上未出现“或”与“且”字,此时应从语句的陈述中搞清含义,从而分清是“p或q”还是“p且q”形式.一般地,若两个命题属于同时都要满足的为“且”,属于并列的为“或”.
9.小李参加全国数学联赛,有三位同学对他作如下的猜测.
甲:小李非第一名,也非第二名;乙:小李非第一名,而是第三名;丙:小李非第三名而是第一名.竞赛结束后发现,一人全猜对,一人猜对一半,一人全猜错,问:小李得了第几名?
解:(1)假设小李得了第三名,则甲全猜对,乙全猜错,显然与题目已知条件相矛盾,故假设不可能.
(2)假设小李得了第二名,则甲猜对一半,乙猜对一半,也与已知条件矛盾,故假设不可能.
(3)假设小李得了第一名,则甲猜对一半,乙全猜错,丙全猜对,无矛盾.
综合(1)(2)(3)知小李得了第一名.
●思悟小结
8.写出下列命题非的形式:
(1)p:函数f(x)=ax2+bx+c的图象与x轴有唯一交点;
(2)q:若x=3或x=4,则方程x2-7x+12=0.
解:(1)函数f(x)=ax2+bx+c的图象与x轴没有交点或至少有两个交点.
(2)若x=3或x=4,则x2-7x+12≠0.
探究创新
7.命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2-4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.
分析:原命题中,a、b为实数是前提,条件是x2+ax+b≤0有非空解集(即不等式有解),结论是a2-4b≥0,由四种命题的关系可得出其他三种命题.
解:逆命题:已知a、b为实数,若a2-4b≥0,则x2+ax+b≤0有非空解集.
否命题:已知a、b为实数,若x2+ax+b≤0没有非空解集,则a2-4b<0.
逆否命题:已知a、b为实数,若a2-4b<0,则x2+ax+b≤0没有非空解集.
原命题、逆命题、否命题、逆否命题均为真命题.
6.(2004年湖北,15)设A、B为两个集合.下列四个命题:
①A B
B 对任意x∈A,有x
对任意x∈A,有x B;②A
B;②A B
B A∩B=
A∩B= ;③A
;③A B
B A
A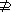 B;④A
B;④A B
B 存在x∈A,使得x
存在x∈A,使得x B.
B.
其中真命题的序号是______________.(把符合要求的命题序号都填上)
解析:A B
B 存在x∈A,有x
存在x∈A,有x B,故①错误;②错误;④正确.
B,故①错误;②错误;④正确.
亦或如下图所示.
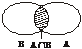
③反例如下图所示.

A B
B A
A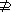 B.反之,同理.
B.反之,同理.
答案:④
5.在一次模拟打飞机的游戏中,小李接连射击了两次,设命题p1“第一次射击击中飞机”,命题p2“第二次射击击中飞机”,试用p1、p2及联结词“或”“且”“非”表示下列命题:
(1)两次都击中飞机;
(2)两次都没击中飞机;
(3)恰有一次击中飞机;
(4)至少有一次击中飞机.
解:(1)两次都击中飞机是p1且p2;
(2)两次都没击中飞机是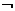 p1且
p1且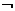 p2;
p2;
(3)恰有一次击中飞机是p1且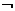 p2,或p2且
p2,或p2且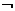 p1;
p1;
(4)至少有一次击中飞机是p1或p2.
培养能力
4.命题“若ab=0,则a、b中至少有一个为零”的逆否命题是_______________.
答案:若a≠0且b≠0,则ab≠0
3.分别用“p或q”“p且q”“非p”填空.
(1)命题“15能被3和5整除”是___________________形式;
(2)命题“16的平方根是4或-4”是______________形式;
(3)命题“李强是高一学生,也是共青团员”是___________________形式.
答案:(1)p且q (2)p或q (3)p且q
2.下列四个命题中真命题是
①“若xy=1,则x、y互为倒数”的逆命题 ②“面积相等的三角形全等”的否命题 ③“若m≤1,则方程x2-2x+m=0有实根”的逆否命题
④“若A∩B=B,则A B”的逆否命题
B”的逆否命题
A.①② B.②③ C.①②③ D.③④
解析:写出满足条件的命题再进行判断.
答案:C
1.如果原命题的结论是“p且q”形式,那么否命题的结论形式为
A.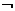 p且
p且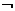 q B.
q B.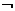 p或
p或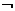 q C.
q C.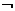 p或
p或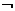 q D.
q D.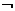 q或
q或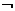 p
p
解析:p且q的否定为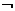 p或
p或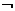 q.
q.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com