8.已知关于x的一元二次方程mx²－4x+4=0，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ①

x²－4mx+4m²－4m－5=0.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　 ②

求使方程①②都有实根的充要条件.

解：方程①有实数根的充要条件是Δ₁=(－4)²－16m≥0，即m≤1；

方程②有实数根的充要条件是Δ₂=(4m)²－4(4m²－4m－5)≥0，即m≥－.

∴方程①②都有实数根的充要条件是－≤m≤1.

7.(2004年湖南，9)设集合U={(x，y)｜x∈R，y∈R}，A={(x，y)|2x－y+m＞0}，B={(x，y)|x+y－n≤0}，那么点P(2，3)∈A∩(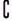_UB)的充要条件是

A.m＞－1，n＜5　　　　　　　　　　　　　　　　　　　　　　 B.m＜－1，n＜5

C.m＞－1，n＞5　　　　　　　　　　　　　　　　　　　　　　 D.m＜－1，n＞5

解析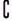：∵_UB={(x，y)｜n＜x+y}，将P(2，3)分别代入集合A、B取交集即可.∴选A.

答案：A

6.已知数列{a_n}的前n项和S_n=pⁿ+q(p≠0且p≠1)，求数列{a_n}成等比数列的充要条件.

分析：先根据前n项和公式，导出使{a_n}为等比数列的必要条件，再证明其充分条件.

解：当n=1时，a₁=S₁=p+q；

当n≥2时，a_n=S_n－S_n－1=(p－1)·p^n－1.

由于p≠0，p≠1，∴当n≥2时，{a_n}是等比数列.要使{a_n}(n∈N^*)是等比数列，则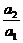=p，即(p－1)·p=p(p+q)，∴q=－1，即{a_n}是等比数列的必要条件是p≠0且p≠1且q=－1.

再证充分性：

当p≠0且p≠1且q=－1时，S_n=pⁿ－1，

a_n=(p－1)·p^n－1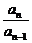，=p(n≥2)，

∴{a_n}是等比数列.

培养能力

5.(2004年北京，5)函数f(x)=x²－2ax－3在区间［1，2］上存在反函数的充分必要条件是

A.a∈(－∞，1］　　　　　　　　　　　　　　　　　　　　　　　　 B.a∈［2，+∞)

C.α∈［1，2］　　　　　　　　　　　　　　　　　　　　　　　 D.a∈(－∞，1］∪［2，+∞)

解析：∵f(x)=x²－2ax－3的对称轴为x=a，∴y=f(x)在［1，2］上存在反函数的充要条件为［1，2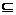］(－∞，a］或［1，2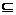］［a，+∞)，即a≥2或a≤1.

答案：D

4.命题A：两曲线F(x，y)＝0和G(x，y)=0相交于点P(x₀，y₀)，命题B：曲线F(x，y)+λG(x，y)＝0(λ为常数)过点P(x₀，y₀)，则A是B的__________条件.

答案：充分不必要

3.(2005年海淀区第一学期期末练习)在△ABC中，“A＞B”是“cosA＜cosB”的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

解析：在△ABC中，A＞BcosA＜cosB(余弦函数单调性).

答案：C

2.(2003年北京高考题)“cos2α=－”是“α=kπ+，k∈Z”的

A.必要不充分条件　　　　　　　　　　　　　　　　　　　　　　　　 B.充分不必要条件

C.充分必要条件　　 　　　　　　　　　　　　　　　　　　　　　 D.既不充分又不必要条件

解析：cos2α=－2α=2kπ±α=kπ±.

答案：A

1.(2004年重庆，7)已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件，那么p是q成立的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

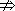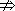解析：依题意有pr，rs，sq，∴prsq.但由于rp，∴qp.

答案：A

5.(2005年春季上海，16)若a、b、c是常数，则“a＞0且b²－4ac＜0”是“对任意x∈R，有ax²+bx+c＞0”的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

解析：若a＞0且b²－4ac＜0，则对任意x∈R，有ax²+bx+c＞0，反之，则不一定成立.如a=0，b=0且c＞0时，也有对任意x∈R，有ax²+bx+c＞0.因此应选A.

答案：A

●典例剖析

[例1] 使不等式2x²－5x－3≥0成立的一个充分而不必要条件是

A.x＜0　　　　　　 　　　　　　　　　　　　　　　　　　 B.x≥0

C.x∈{－1，3，5}　　　　　　　　　　　　　　　　　　　　　 D.x≤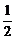－或x≥3

剖析：∵2x²－5x－3≥0成立的充要条件是x≤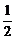－或x≥3，∴对于A当x=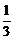－时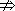2x²－5x－3≥0.同理其他也可用特殊值验证.

答案：C

[例2] 求证：关于x的方程ax²+bx+c=0有一根为1的充分必要条件是a+b+c=0.

证明：(1)必要性，即“若x=1是方程ax²+bx+c=0的根，则a+b+c=0”.

∵x=1是方程的根，将x=1代入方程，得a·1²+b·1+c=0，即a+b+c=0.

(2)充分性，即“若a+b+c=0，则x=1是方程ax²+bx+c=0的根”.

把x=1代入方程的左边，得a·1²+b·1+c=a+b+c.∵a+b+c=0，∴x=1是方程的根.

综合(1)(2)知命题成立.

深化拓展

求ax²+2x+1=0(a≠0)至少有一负根的充要条件.

证明：必要性：

(1)方程有一正根和一负根，等价于

a＜0.

(2)方程有两负根，等价于

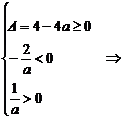0＜a≤1.

综上可知，原方程至少有一负根的必要条件是a＜0或0＜a≤1.

充分性：由以上推理的可逆性，知当a＜0时方程有异号两根；当0＜a≤1时，方程有两负根.故a＜0或0＜a≤1是方程ax²+2x+1=0至少有一负根的充分条件.

答案：a＜0或0＜a≤1.

[例3] 下列说法对不对?如果不对，分析错误的原因.

(1)x²＝x+2是x=x²的充分条件；

(2)x²＝x+2是x=x²的必要条件.

解：(1)x²=x+2是x=x²的充分条件是指x²=x+2x=x².

但这里“”不成立，因为x=－1时，“”左边为真，但右边为假.得出错误结论的原因可能是应用了错误的推理：

x²=x+2x=x²=x.

这里推理的第一步是错误的(请同学补充说明具体错在哪里).

(2)x²=x+2是x=x²的必要条件是指x=x²x²=x+2.

但这里“”不成立，因为x=0时，“”左边为真，但右边为假.得出错误结论的原因可能是用了错误的推理:

x=x²=xx+2=x².

这里推理的第一步是错误的(请同学补充说明具体错在哪里).

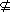评述：此题的解答比较注重逻辑推理.事实上，也可以从真值集合方面来分析：x²=x+2的真值集合是{－1，2}，x=x²的真值集合是{0，2}，{－1，2}{0，2}，而{0，2} 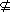{－1，2}，所以(1)(2)两个结论都不对.

●闯关训练

夯实基础

4.若条件p:a＞4，q:5＜a＜6，则p是q的______________.

解析：a＞4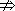5＜a＜6，如a=7虽然满足a＞4，但显然a不满足5＜a＜6.

答案：必要不充分条件