3.掌握二项式定理和二项展开式的性质，并能用它们计算和证明一些简单的问题.

●复习方略指南

排列与组合是高中数学中，从内容到方法都比较独特的一部分.其重点是在熟练应用公式的基础上，运用两个基本原理，解决计数应用题.

二项式定理的重点是二项展开式及通项公式的联系和应用.

本章内容高考所占比重不大，经常以选择题、填空题的形式出现，但对思维能力要求较高，在复习中，要注意通过典型例题，掌握分析问题的方法，总结解题规律.

2.理解排列与组合的意义，掌握排列数与组合数的计算公式，掌握组合数的两个性质，并能用它们解决一些简单的应用问题.

1.掌握分类计数原理与分步计数原理，并能用它们分析和解决一些简单的应用问题.

3.要证明充要性应从充分性、必要性两个方面来证.

拓展题例

[例题] 指出下列命题中，p是q的什么条件.

(1)p:0＜x＜3，q:|x－1|＜2；

(2)p:(x－2)(x－3)=0，q:x=2；

(3)p:c=0，q:抛物线y=ax²+bx+c过原点.

解：(1)p:0＜x＜3，q:－1＜x＜3.

p是q的充分但不必要条件.

(2)p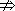q，qp.p是q的必要但不充分条件.

(3)p是q的充要条件.

评述：依集合的观点看，若AB，则A是B的充分条件，B是A的必要条件；若A=B，则A是B的充要条件.

2.强调反证法的第一步，要与否命题分清.

1.掌握常用反证法证题的题型，如含有“至少有一个”“至多有一个”等字眼多用反证法.

2.证明充要性要从充分性、必要性两个方面来证明.

●教师下载中心

教学点睛

1.要注意一些常用的“结论否定形式”，如“至少有一个”“至多有一个”“都是”的否定形式是“一个也没有”“至少有两个”“不都是”.

10.若x、y、z均为实数，且a=x²－2y+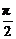，b=y²－2z+，c=z²－2x+，则a、b、c中是否至少有一个大于零？请说明理由.

解：假设a、b、c都不大于0，即a≤0，b≤0，c≤0，则a+b+c≤0.

而a+b+c=x²－2y+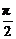+y²－2z++z²－2x+=(x－1)²+(y－1)²+(z－1)²+π－3，

∵π－3＞0，且无论x、y、z为何实数，

(x－1)²+(y－1)²+(z－1)²≥0，

∴a+b+c＞0.这与a+b+c≤0矛盾.因此，a、b、c中至少有一个大于0.

●思悟小结

9.已知a、b、c是互不相等的非零实数.

求证：三个方程ax²+2bx+c=0，bx²+2cx+a=0，cx²+2ax+b=0至少有一个方程有两个相异实根.

证明：反证法：

假设三个方程中都没有两个相异实根，

则Δ₁=4b²－4ac≤0，Δ₂=4c²－4ab≤0，Δ₃=4a²－4bc≤0.

相加有a²－2ab+b²+b²－2bc+c²+c²－2ac+a²≤0，

(a－b)²+(b－c)²+(c－a)²≤0.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 ①

由题意a、b、c互不相等，∴①式不能成立.

∴假设不成立，即三个方程中至少有一个方程有两个相异实根.

探究创新