
1.从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植.不同的种植方法共有
A.24种 B.18种 C.12种 D.6种
解析:∵黄瓜必选,故再选2种蔬菜的方法数是C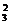 种,在不同土质的三块土地上种植的方法是A
种,在不同土质的三块土地上种植的方法是A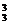 .
.
∴种法共有C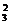 ·A
·A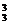 =18种.
=18种.
答案:B
5.市内某公共汽车站有10个候车位(成一排),现有4名乘客随便坐在某个座位上候车,则恰好有5个连续空座位的候车方式共有_____________种.(用数字作答)
解析:把四位乘客当作4个元素作全排列有A 种排法,将一个空位和余下的4个空位作为一个元素插空有A
种排法,将一个空位和余下的4个空位作为一个元素插空有A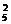 种排法.∴A
种排法.∴A ·A
·A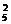 =480.
=480.
答案:480
●典例剖析
[例1] 从6名短跑运动员中选4人参加4×100 m接力,如果其中甲不能跑第一棒,乙不能跑第四棒,问共有多少种参赛方法?
解法一:问题分成三类:(1)甲、乙两人均不参加,有A 种;(2)甲、乙两人有且仅有一人参加,有2C
种;(2)甲、乙两人有且仅有一人参加,有2C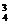 (A
(A -A
-A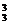 )种;(3)甲、乙两人均参加,有C
)种;(3)甲、乙两人均参加,有C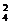 (A
(A -2A
-2A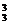 +A
+A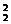 )种.故共有252种.
)种.故共有252种.
解法二:六人中取四人参加的种数为A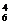 ,除去甲、乙两人中至少有一人不排在恰当位置的有C
,除去甲、乙两人中至少有一人不排在恰当位置的有C A
A 种,因前后把甲、乙两人都不在恰当位置的种数A
种,因前后把甲、乙两人都不在恰当位置的种数A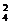 减去了两次.故共有A
减去了两次.故共有A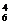 -C
-C A
A +A
+A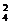 =252种.
=252种.
评述:对于带有限制条件的排列、组合综合题,一般用分类讨论或间接法两种方法处理.
[例2] 对某种产品的6件不同正品和4件不同次品一一进行测试,至区分出所有次品为止.若所有次品恰好在第5次测试时被全部发现,则这样的测试方法有多少种可能?
解:C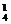 (C
(C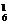 C
C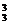 )A
)A =576,第5次必测出一次品,余下3件在前4次被测出,从4件中确定最后一件品有C
=576,第5次必测出一次品,余下3件在前4次被测出,从4件中确定最后一件品有C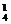 种方法,前4次中应有1正品、3次品,有C
种方法,前4次中应有1正品、3次品,有C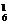 C
C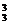 种,前4次测试中的顺序有A
种,前4次测试中的顺序有A 种,由分步计数原理即得.
种,由分步计数原理即得.
评述:本题涉及一类重要问题,即问题中既有元素的限制,又有排列的问题,一般是先选元素(即组合)后排列.
思考讨论
用类似的方法,讨论如下问题.
某种产品有5件不同的正品,4件不同的次品,现在一件件地进行检测,直到4件次品全部测出为止,则最后一件次品恰好在第6次检测时被测出,这样的检测方案有多少种?
提示:问题相当于从10件产品中取出6件的一个排列,第6位为次品,前五位有其余3件次品,可分三步:先从4件产品中留出1件次品排第6位,有4种方法;再从5件正品中取2件,有C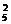 种方法;再把3件次品和取出的2件正品排在前五位有A
种方法;再把3件次品和取出的2件正品排在前五位有A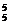 种方法.所以检测方案种数为4×C
种方法.所以检测方案种数为4×C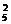 ·A
·A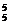 =4800.
=4800.
[例3] 在一块并排10垄的田地中,选择2垄分别种植A、B两种作物,每种作物种植一垄.为有利于作物生长,要求A、B两种作物的间隔不小于6垄,则不同的种植方法共有多少种?
解:依题意,A、B两种作物的间隔至少6垄,至多8垄.(1)间隔6垄时,有3×A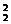 种;(2)间隔7垄时,有2×A
种;(2)间隔7垄时,有2×A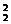 种.(3)间隔8垄时,有A
种.(3)间隔8垄时,有A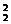 种.所以共有3A
种.所以共有3A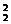 +2A
+2A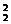 +A
+A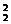 =12种种植方法.
=12种种植方法.
[例4] 有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是
A.234 B.346 C.350 D.363
解法一:分类讨论法.
(1)前排一个,后排一个,2C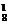 ·C
·C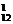 =192.
=192.
(2)后排坐两个(不相邻),
2(10+9+8+…+1)=110.
(3)前排坐两个,2·(6+5+…+1)+2=44个.
∴总共有192+110+44=346个.
解法二:考虑中间三个位置不坐,4号座位与8号座位不算相邻.
∴总共有A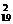 +2+2=346个.
+2+2=346个.
答案:B
评述:本题考查分类讨论在解排列组合应用题中的运用.这是一道难度较大的小综合题.
●闯关训练
夯实基础
4.从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字组成没有重复数字的四位数,其中能被5整除的四位数共有_____________个.(用数字作答)
解析:①四位数中包含5和0的情况:
C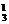 ·C
·C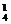 ·(A
·(A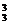 +A
+A ·A
·A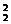 )=120.
)=120.
②四位数中包含5,不含0的情况:
C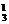 ·C
·C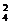 ·A
·A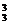 =108.
=108.
③四位数中包含0,不含5的情况:
C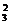 C
C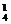 A
A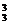 =72.
=72.
综上,四位数总数为120+108+72=300.
答案:300
3.5本不同的书,全部分给四个学生,每个学生至少1本,不同分法的种数为
A.480 B.240 C.120 D.96
解析:先把5本书中的两本捆起来(C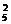 ),再分成四份(A
),再分成四份(A ),∴分法种数为C
),∴分法种数为C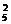 ·A
·A =240.
=240.
答案:B
2.从5名学生中选出4名分别参加数学、物理、化学、外语竞赛,其中A不参加物理、化学竞赛,则不同的参赛方案种数为
A.24 B.48 C.120 D.72
解析:若不含A,则有A 种;若含有A,则有C
种;若含有A,则有C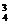 ·C
·C ·A
·A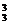 种.∴A
种.∴A +C
+C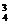 ·C
·C ·A
·A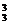 =72.
=72.
答案:D
1.(2004年福建,理6)某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为
A.A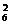 C
C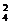 B.
B. A
A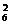 C
C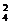 C.A
C.A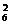 A
A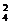 D.2A
D.2A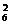
解析:将4名学生均分成两组,方法数为 C
C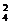 ,再分配给6个年级中的2个,分配方法数为A
,再分配给6个年级中的2个,分配方法数为A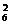 ,∴合要求的安排方法数为
,∴合要求的安排方法数为 C
C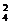 ·A
·A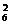 .
.
答案:B
2.解排列组合的应用题,要注意四点:
(1)仔细审题,判断是组合问题还是排列问题;要按元素的性质分类,按事件发生的过程进行分步.
(2)深入分析、严密周详,注意分清是乘还是加,既不少也不多,辩证思维,多角度分析,全面考虑,这不仅有助于提高逻辑推理能力,也尽可能地避免出错.
(3)对于附有条件的比较复杂的排列组合应用题,要周密分析,设计出合理的方案,把复杂问题分解成若干简单的基本问题后应用分类计数原理或分步计数原理来解决.
(4)由于排列组合问题的答案一般数目较大,不易直接验证,因此在检查结果时,应着重检查所设计的解决问题的方案是否完备,有无重复或遗漏,也可采用多种不同的方法求解,看看是否相同.在对排列组合问题分类时,分类标准应统一,否则易出现遗漏或重复.
●点击双基
1.排列、组合都是研究事物在某种给定的模式下所有可能的配置的数目问题,它们之间的主要区别在于是否要考虑选出元素的先后顺序,不需要考虑顺序的是组合问题,需要考虑顺序的是排列问题,排列是在组合的基础上对入选的元素进行排队,因此,分析解决排列组合问题的基本思维是“先组,后排”.
10.4 排列与组合的综合问题
●知识梳理
2.熟练掌握组合数公式的两种形式.
拓展题例
[例题] 某篮球队共7名老队员,5名新队员,根据下列情况分别求出有多少种不同的出场阵容.
(1)某老队员必须上场,某2新队员不能出场;
(2)有6名打前锋位,4名打后卫位,甲、乙两名既能打前锋又能打后卫位.
解:(1)C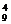 =126种.
=126种.
(2)以2名既擅长前锋位又能打后卫位的队员是否上场,且上场后是前锋还是后卫作分类标准:①甲、乙都不上场有C C
C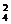 =120种;②甲、乙有一名上场,作前锋位有C
=120种;②甲、乙有一名上场,作前锋位有C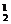 (C
(C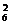 C
C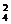 )种,作后卫位有C
)种,作后卫位有C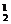 (C
(C C
C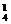 )种,共C
)种,共C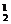 (C
(C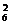 C
C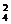 )+C
)+C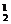 (C
(C C
C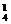 )=340种;③甲、乙都上场,有C
)=340种;③甲、乙都上场,有C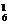 C
C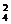 +C
+C C
C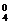 +C
+C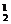 (C
(C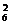 C
C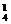 )=176种.据分类计数原理,共有120+340+176=636种.
)=176种.据分类计数原理,共有120+340+176=636种.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com