
4.从编号为1,2,3,4,5,6,7,8,9,10的十个球中,任取5个球,则这5个球编号之和为奇数的概率是________.
解析:任取5个球有C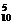 种结果,编号之和为奇数的结果数为C
种结果,编号之和为奇数的结果数为C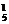 C
C +C
+C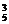 C
C +C
+C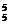 =126,故所求概率为
=126,故所求概率为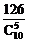 =
= .
.
答案:
3.有3人,每人都以相同的概率被分配到4个房间中的一间,则至少有2人分配到同一房间的概率是________.
解析:P=1- =
= .
.
答案: 
2.一批产品共10件,其中有两件次品,现随机地抽取5件,则所取5件中至多有一件次品的概率为
A. B.
B.
C. D.
D.
解析:P= +
+ =
=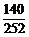 +
+ =
= .
.
答案:B
1.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是
A.至少有1个白球,都是红球 B.至少有1个白球,至多有1个红球
C.恰有1个白球,恰有2个白球 D.至多有1个白球,都是红球
答案:C
5.有10张人民币,其中伍元的有2张,贰元的有3张,壹元的有5张,从中任取3张,则3张中至少有2张的币值相同的概率为________.
解析:至少2张相同,则分2张时和3张时,故P= =
= .
.
答案: 
●典例剖析
[例1] 今有标号为1,2,3,4,5的五封信,另有同样标号的五个信封.现将五封信任意地装入五个信封,每个信封装入一封信,试求至少有两封信配对的概率.
解:设恰有两封信配对为事件A,恰有三封信配对为事件B,恰有四封信(也即五封信配对)为事件C,则“至少有两封信配对”事件等于A+B+C,且A、B、C两两互斥.
∵P(A)= ,P(B)=
,P(B)= ,P(C)=
,P(C)= ,
,
∴所求概率P(A)+P(B)+P(C)= .
.
答:至少有两封信配对的概率是 .
.
思考讨论
若求(1)至少有1封信配对.
答案: .
.
(2)没有一封信配对.
答案:1- .
.
[例2] (2004年合肥模拟题)在袋中装20个小球,其中彩球有n个红色、5个蓝色、10个黄色,其余为白球.
求:(1)如果从袋中取出3个都是相同颜色彩球(无白色)的概率是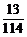 ,且n≥2,那么,袋中的红球共有几个?
,且n≥2,那么,袋中的红球共有几个?
(2)根据(1)的结论,计算从袋中任取3个小球至少有一个是红球的概率.
解:(1)取3个球的种数为C =1140.
=1140.
设“3个球全为红色”为事件A,“3个球全为蓝色”为事件B,“3个球全为黄色”为事件C.
P(B)= =
= ,P(C)=
,P(C)=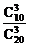 =
= .
.
∵A、B、C为互斥事件,
∴P(A+B+C)=P(A)+P(B)+P(C),
即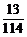 =P(A)+
=P(A)+ +
+
 P(A)=0
P(A)=0 取3个球全为红球的个数≤2.
取3个球全为红球的个数≤2.
又∵n≥2,故n=2.
(2)记“3个球中至少有一个是红球”为事件D.则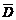 为“3个球中没有红球”.
为“3个球中没有红球”.
P(D)=1-P(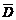 )=1-
)=1- =
=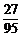 或
或
P(D)= =
=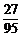 .
.
[例3] 9个国家乒乓球队中有3个亚洲国家队,抽签分成甲、乙、丙三组(每组3队)进行预赛,试求:
(1)三个组各有一个亚洲队的概率;
(2)至少有两个亚洲队分在同一组的概率.
解:9个队分成甲、乙、丙三组有C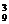 C
C C
C 种等可能的结果.(1)三个亚洲国家队分给甲、乙、丙三组,每组一个队有A
种等可能的结果.(1)三个亚洲国家队分给甲、乙、丙三组,每组一个队有A 种分法,其余6个队平分给甲、乙、丙三组有C
种分法,其余6个队平分给甲、乙、丙三组有C C
C C
C 种分法.故三个组各有一个亚洲国家队的结果有A
种分法.故三个组各有一个亚洲国家队的结果有A ·C
·C C
C C
C 种,所求概率
种,所求概率
P(A)= =
=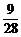 .
.
答:三个组各有一个亚洲国家队的概率是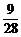 .
.
(2)∵事件“至少有两个亚洲国家队分在同一组”是事件“三个组各有一个亚洲国家队”的对立事件,∴所求概率为1-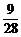 =
= .
.
答:至少有两个亚洲国家队分在同一组的概率是 .
.
●闯关训练
夯实基础
4.(2004年东北三校模拟题)一个口袋中装有大小相同的2个白球和3个黑球,从中摸出一个球,放回后再摸出一个球,则两次摸出的球恰好颜色不同的概率为________.
解析:(1)先摸出白球,P白=C ,再摸出黑球,P白黑=C
,再摸出黑球,P白黑=C C
C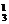 ;(2)先摸出黑球,P黑=C
;(2)先摸出黑球,P黑=C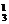 ,再摸出白球,P黑白=C
,再摸出白球,P黑白=C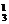 C
C ,故P=
,故P= +
+ =
= .
.
答案:
3.甲、乙两人下棋,甲获胜的概率是40%,甲不输的概率为90%,则甲、乙二人下成和棋的概率为
A.60% B.30% C.10% D.50%
解析:甲不输即为甲获胜或甲、乙二人下成和棋,90%=40%+p,∴p=50%.
答案:D
2.从一批羽毛球产品中任取一个,质量小于4.8 g的概率是0.3,质量不小于4.85 g的概率是0.32,那么质量在[4.8,4.85)g范围内的概率是
A.0.62 B.0.38 C.0.7 D.0.68
解析:设一个羽毛球的质量为ξ g,则
P(ξ<4.8)+P(4.8≤ξ<4.85)+P(ξ≥4.85)=1.
∴P(4.8≤ξ<4.85)=1-0.3-0.32=0.38.
答案:B
1.两个事件互斥是这两个事件对立的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:根据定义判断.
答案:B
5.分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想.
●点击双基
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com