
2.独立重复实验:如果在一次试验中某事件发生的概率为p,那么在n次独立重复试验中,这个事件恰好发生k次的概率为Pn(k)=C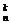 pk(1-p)n-k.
pk(1-p)n-k.
1.相互独立事件:事件A是否发生对事件B发生的概率没有影响,这样的两个事件叫相互独立事件.
11.3 相互独立事件同时发生的概率
●知识梳理
2.如果某事件A发生包含的情况较多,而它的对立事件(即A不发生)所包含的情形较少,利用公式P(A)=1-P(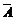 )计算A的概率则比较方便.这不仅体现逆向思维,同时对培养思维的灵活性是非常有益的.
)计算A的概率则比较方便.这不仅体现逆向思维,同时对培养思维的灵活性是非常有益的.
拓展题例
[例题] 某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点,如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;
(2)停车的次数不少于2次;
(3)恰好停车2次.
解:将8个职工每一种下车的情况作为1个基本事件,那么共有38=6561(个)基本事件.
(1)记“该车在某停车点停车”为事件A,事件A发生说明在这个停车点有人下车,即至少有一人下车,这个事件包含的基本事件较复杂,于是我们考虑它的对立事件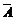 ,即“8个人都不在这个停车点下车,而在另外2个点中的任一个下车”.
,即“8个人都不在这个停车点下车,而在另外2个点中的任一个下车”.
∵P(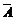 )=
)= =
=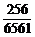 ,
,
∴P(A)=1-P(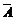 )=1-
)=1-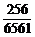 =
=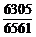 .
.
(2)记“停车的次数不少于2次”为事件B,则“停车次数恰好1次”为事件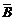 ,则P(B)=1-P(
,则P(B)=1-P(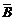 )=1-
)=1- =1-
=1- =
=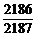 .
.
(3)记“恰好停车2次”为事件C,事件C发生就是8名职工在其中2个停车点下车,每个停车点至少有1人下车,所以该事件包含的基本事件数为C (C
(C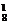 +C
+C +C
+C +…+C
+…+C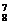 )=3×(28-2)=3×254,于是P(C)=
)=3×(28-2)=3×254,于是P(C)=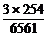 =
= .
.
1.概率加法公式仅适用于互斥事件,即当A、B互斥时,P(A+B)=P(A)+P(B),否则公式不能使用.
9.有点难度哟!
有人玩掷硬币走跳棋的游戏,已知硬币出现正反面为等可能性事件,棋盘上标有第0站,第1站,第2站,…,第100站,一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面,棋向前跳一站(从k到k+1),若掷出反面,棋向前跳两站(从k到k+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束.设棋子跳到第n站概率为Pn.
(1)求P0,P1,P2的值;
(2)求证:Pn-Pn-1=- (Pn-1-Pn-2),其中n∈N,2≤n≤99;
(Pn-1-Pn-2),其中n∈N,2≤n≤99;
(3)求P99及P100的值.
(1)解:棋子开始在第0站为必然事件,∴P0=1.
第一次掷硬币出现正面,棋子跳到第1站,其概率为 ,
,
∴P1= .棋子跳到第2站应从如下两方面考虑:
.棋子跳到第2站应从如下两方面考虑:
①前两次掷硬币都出现正面,其概率为 ;
;
②第一次掷硬币出现反面,其概率为 .
.
∴P2= +
+ =
= .
.
(2)证明:棋子跳到第n(2≤n≤99)站的情况是下列两种,而且也只有两种:
①棋子先到第n-2站,又掷出反面,其概率为 Pn-2;
Pn-2;
②棋子先到第n-1站,又掷出正面,其概率为 Pn-1.
Pn-1.
∴Pn= Pn-2+
Pn-2+ Pn-1.
Pn-1.
∴Pn-Pn-1=- (Pn-1-Pn-2).
(Pn-1-Pn-2).
(3)解:由(2)知,当1≤n≤99时,数列{Pn-Pn-1}是首项为P1-P0=- ,公比为-
,公比为- 的等比数列.
的等比数列.
∴P1-1=- ,P2-P1=(-
,P2-P1=(- )2,P3-P2=(-
)2,P3-P2=(- )3,…,Pn-Pn-1=(-
)3,…,Pn-Pn-1=(- )n.
)n.
以上各式相加,得Pn-1=(- )+(-
)+(- )2+…+(-
)2+…+(- )n,
)n,
∴Pn=1+(- )+(-
)+(- )2+…+(-
)2+…+(- )n=
)n=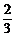 [1-(-
[1-(- )n+1](n=0,1,2,…,99).
)n+1](n=0,1,2,…,99).
∴P99=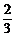 [1-(
[1-( )100],
)100],
P100= P98=
P98= ·
·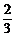 [1-(-
[1-(- )99]=
)99]= [1+(
[1+( )99].
)99].
●思悟小结
求某些稍复杂的事件的概率时,通常有两种方法:一是将所求事件的概率化成一些彼此互斥的事件的概率的和;二是先去求此事件的对立事件的概率.
●教师下载中心
教学点睛
8.8个篮球队中有2个强队,先任意将这8个队分成两个组(每组4个队)进行比赛,则这两个强队被分在一个组内的概率是________.
解法一:2个强队分在同一组,包括互斥的两种情况:2个强队都分在A组和都分在B组.2个强队都分在A组,可看成“从8个队中抽取4个队,里面包括2个强队”这一事件,其概率为 ;2个强队都分在B组,可看成“从8个队中抽取4个队,里面没有强队”这一事件,其概率为
;2个强队都分在B组,可看成“从8个队中抽取4个队,里面没有强队”这一事件,其概率为 .因此,2个强队分在同一个组的概率为P=
.因此,2个强队分在同一个组的概率为P= +
+ =
= .
.
解法二:“2个强队分在同一个组”这一事件的对立事件“2个组中各有一个强队”,而两个组中各有一个强队,可看成“从8个队中抽取4个队,里面恰有一个强队”这一事件,其概率为 .因此,2个强队分在同一个组的概率P=1-
.因此,2个强队分在同一个组的概率P=1- =1-
=1-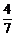 =
= .
.
答案:
探究创新
7.某单位36人的血型类型是:A型12人,B型10人,AB型8人,O型6人.现从这36人中任选2人.
求:(1)两人同为A型血的概率;
(2)两人具有不相同血型的概率.
解:(1)P= =
= .
.
(2)考虑对立事件:两人同血型为事件A,
那么P(A)=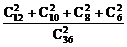 =
= .
.
所以不同血型的概率为P=1-P(A)= .
.
6.袋中有5个白球,3个黑球,从中任意摸出4个,求下列事件发生的概率:
(1)摸出2个或3个白球;
(2)至少摸出1个白球;
(3)至少摸出1个黑球.
解:从8个球中任意摸出4个共有C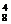 种不同的结果.记从8个球中任取4个,其中恰有1个白球为事件A1,恰有2个白球为事件A2,3个白球为事件A3,4个白球为事件A4,恰有i个黑球为事件Bi.则
种不同的结果.记从8个球中任取4个,其中恰有1个白球为事件A1,恰有2个白球为事件A2,3个白球为事件A3,4个白球为事件A4,恰有i个黑球为事件Bi.则
(1)摸出2个或3个白球的概率
P1=P(A2+A3)=P(A2)+P(A3)=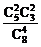 +
+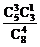 =
= +
+ =
= .
.
(2)至少摸出1个白球的概率
P2=1-P(B4)=1-0=1.
(3)至少摸出1个黑球的概率
P3=1-P(A4)=1- =
=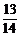 .
.
培养能力
5.52张桥牌中有4张A,甲、乙、丙、丁每人任意分到13张牌,已知甲手中有一张A,求丙手中至少有一张A的概率.
解:丙手中没有A的概率是 ,由对立事件概率的加法公式知,丙手中至少有一张A的概率是1-
,由对立事件概率的加法公式知,丙手中至少有一张A的概率是1- =0.5949.
=0.5949.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com