
2.在某段时间内,甲地不下雨的概率为0.3,乙地不下雨的概率为0.4,假设在这段时间内两地是否下雨相互无影响,则这段时间内两地都下雨的概率是
A.0.12 B.0.88 C.0.28 D.0.42
解析:P=(1-0.3)(1-0.4)=0.42.
答案:D
1.若A与B相互独立,则下面不相互独立事件有
A.A与 B.A与
B.A与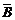 C.
C.  与B D.
与B D.  与
与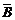
解析:由定义知,易选A.
答案:A
5.一出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
解析:因为这位司机在第一、二个交通岗未遇到红灯,在第三个交通岗遇到红灯,所以P=(1- )(1-
)(1- )×
)× =
=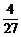 .
.
答案: 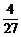
●典例剖析
[例1] (2004年广州模拟题)某班有两个课外活动小组,其中第一小组有足球票6张,排球票4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,乙从第二小组的10张票中任抽1张.
(1)两人都抽到足球票的概率是多少?
(2)两人中至少有1人抽到足球票的概率是多少?
解:记“甲从第一小组的10张票中任抽1张,抽到足球票”为事件A,“乙从第二小组的10张票中任抽1张,抽到足球票”为事件B;记“甲从第一小组的10张票中任抽1张,抽到排球票”为事件 ,“乙从第二小组的10张票中任抽1张,抽到排球票”为事件
,“乙从第二小组的10张票中任抽1张,抽到排球票”为事件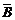 ,
,
于是P(A)= =
=  ,P(
,P( )=
)= ;
;
P(B)= =
=  ,P(
,P(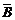 )=
)= .
.
由于甲(或乙)是否抽到足球票,对乙(或甲)是否抽到足球票没有影响,因此A与B是相互独立事件.
(1)甲、乙两人都抽到足球票就是事件A·B发生,根据相互独立事件的概率乘法公式,得到P(A·B)=P(A)·P(B)= ·
· =
= .
.
答:两人都抽到足球票的概率是 .
.
(2)甲、乙两人均未抽到足球票(事件 ·
·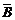 发生)的概率为
发生)的概率为
P( ·
·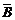 )=P(
)=P( )·P(
)·P(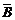 )=
)= ·
· =
= .
.
∴两人中至少有1人抽到足球票的概率为
P=1-P( ·
·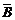 )=1-
)=1- =
=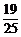 .
.
答:两人中至少有1人抽到足球票的概率是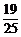 .
.
[例2] 有外形相同的球分别装在三个不同的盒子中,每个盒子中有10个球.其中第一个盒子中有7个球标有字母A,3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中有红球8个,白球2个.试验按如下规则进行:先在第一个盒子中任取一个球,若取得标有字母A的球,则在第二个盒子中任取一球;若第一次取得标有字母B的球,则在第三个盒子中任取一球.如果第二次取得的球是红球,则称试验成功,求试验成功的概率.
解:设事件A:从第一个盒子中取得一个标有字母A的球;事件B:从第一个盒子中取得一个标有字母B的球,则A、B互斥,且P(A)= ,P(B)=
,P(B)= ;事件C:从第二号盒子中取一个红球,事件D:从第三号盒子中取一个红球,则C、D互斥,且P(C)=
;事件C:从第二号盒子中取一个红球,事件D:从第三号盒子中取一个红球,则C、D互斥,且P(C)= ,P(D)=
,P(D)= =
=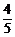 .
.
显然,事件A·C与事件B·D互斥,且事件A与C是相互独立的,B与D也是相互独立的.所以试验成功的概率为P=P(A·C+B·D)=P(A·C)+P(B·D)=P(A)·P(C)+P(B)·P(D)= .
.
∴本次试验成功的概率为 .
.
[例3] (2004年福州模拟题)冰箱中放有甲、乙两种饮料各5瓶,每次饮用时从中任意取1瓶甲种或乙种饮料,取用甲种或乙种饮料的概率相等.
(1)求甲种饮料饮用完毕而乙种饮料还剩下3瓶的概率;
(2)求甲种饮料被饮用瓶数比乙种饮料被饮用瓶数至少多4瓶的概率.
解:(1)由题意知,甲种已饮用5瓶,乙种已饮用2瓶.
记“饮用一次,饮用的是甲种饮料”为事件A,
则p=P(A)= .
.
题(1)即求7次独立重复试验中事件A发生5次的概率为P7(5)=C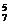 p5(1-p)2=C
p5(1-p)2=C (
( )7=
)7= .
.
(2)有且仅有3种情形满足要求:
甲被饮用5瓶,乙被饮用1瓶;甲被饮用5瓶,乙没有被饮用;甲被饮用4瓶,乙没有被饮用.
所求概率为P6(5)+P5(5)+P4(4)=C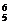 p5(1-p)+C
p5(1-p)+C p5+C
p5+C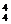 p4=
p4= .
.
答:甲饮料饮用完毕而乙饮料还剩3瓶的概率为 ,甲饮料被饮用瓶数比乙饮料被饮用瓶数至少多4瓶的概率为
,甲饮料被饮用瓶数比乙饮料被饮用瓶数至少多4瓶的概率为 .
.
●闯关训练
夯实基础
4.一道数学竞赛试题,甲生解出它的概率为 ,乙生解出它的概率为
,乙生解出它的概率为 ,丙生解出它的概率为
,丙生解出它的概率为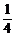 ,由甲、乙、丙三人独立解答此题只有一人解出的概率为________.
,由甲、乙、丙三人独立解答此题只有一人解出的概率为________.
解析:P= ×
× ×
×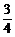 +
+  ×
× ×
×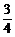 +
+  ×
× ×
×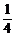 =
= .
.
答案: 
3.从应届高中生中选出飞行员,已知这批学生体型合格的概率为 ,视力合格的概率为
,视力合格的概率为 ,其他几项标准合格的概率为
,其他几项标准合格的概率为 ,从中任选一学生,则该生三项均合格的概率为(假设三项标准互不影响)
,从中任选一学生,则该生三项均合格的概率为(假设三项标准互不影响)
A. B.
B. C.
C.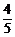 D.
D.
解析:P= ×
× ×
× =
= .
.
答案:C
2.将一枚硬币连掷5次,如果出现k次正面的概率等于出现k+1次正面的概率,那么k的值为
A.0 B.1 C.2 D.3
解析:由C (
( )k(
)k( )5-k=C
)5-k=C (
( )k+1·(
)k+1·( )5-k-1,
)5-k-1,
即C =C
=C ,k+(k+1)=5,k=2.
,k+(k+1)=5,k=2.
答案:C
1.(2004年辽宁,5)甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率是p2,那么恰好有1人解决这个问题的概率是
A.p1p2 B.p1(1-p2)+p2(1-p1)
C.1-p1p2 D.1-(1-p1)(1-p2)
解析:恰有一人解决就是甲解决乙没有解决或甲没有解决乙解决,故所求概率是p1(1-p2)+p2(1-p1).
答案:B
5.事件A与B的积记作A·B,A·B表示这样一个事件,即A与B同时发生.
当A和B是相互独立事件时,事件A·B满足乘法公式P(A·B)=P(A)·P(B),还要弄清 ·
·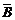 ,
, 的区别.
的区别.  ·
·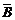 表示事件
表示事件 与
与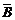 同时发生,因此它们的对立事件A与B同时不发生,也等价于A与B至少有一个发生的对立事件即
同时发生,因此它们的对立事件A与B同时不发生,也等价于A与B至少有一个发生的对立事件即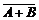 ,因此有
,因此有 ·
·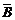 ≠
≠ ,但
,但 ·
·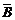 =
=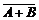 .
.
●点击双基
4.互斥事件与相互独立事件是有区别的:
两事件互斥是指同一次试验中两事件不能同时发生,两事件相互独立是指不同试验下,二者互不影响;两个相互独立事件不一定互斥,即可能同时发生,而互斥事件不可能同时发生.
3.关于相互独立事件也要抓住以下特征加以理解:
第一,相互独立也是研究两个事件的关系;
第二,所研究的两个事件是在两次试验中得到的;
第三,两个事件相互独立是从“一个事件的发生对另一个事件的发生的概率没有影响”来确定的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com