
2.某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上的人,用分层抽样法从中抽取20人,各年龄段分别抽取的人数为
A.7,5,8 B.9,5,6
C.6,5,9 D.8,5,7
解析:45×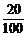 =
= ×45=9,25×
×45=9,25×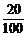 =5,30×
=5,30× =6.
=6.
答案:B
5.某班学生在一次数学考试中成绩分布如下表:
|
分数段 |
[0,80) |
[80,90) |
[90,100) |
||
|
人数 |
2 |
|
6 |
||
|
分数段 |
[100,110) |
[110,120 |
[120,130) |
||
|
人数 |
8 |
12 |
6 |
||
|
分数段 |
[130,140) |
[140,150) |
|
||
|
人数 |
4 |
2 |
|
那么分数在[100,110)中的频率和分数不满110分的累积频率分别是______________、_______(精确到0.01).
解析:由频率计算方法知:总人数=45.
分数在[100,110)中的频率为 =0.178≈0.18.
=0.178≈0.18.
分数不满110分的累积频率为 =
= ≈0.47.
≈0.47.
答案:0.18 0.47
●典例剖析
[例1] (2004年湖南,5)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
剖析:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
依据题意,第①项调查应采用分层抽样法、第②项调查应采用简单随机抽样法.故选B.
答案:B
评述:采用什么样的抽样方法要依据研究的总体中的个体情况来定.
[例2] (2004年福建,15)一个总体中有100个个体,随机编号为0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k小组中抽取的号码个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是___________.
剖析:此问题总体中个体的个数较多,因此采用系统抽样.按题目中要求的规则抽取即可.
∵m=6,k=7,m+k=13,∴在第7小组中抽取的号码是63.
答案:63
评述:当总体中个体个数较多而差异又不大时可采用系统抽样.采用系统抽样在每小组内抽取时应按规则进行.
[例3] 把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的累积频率为0.79,而剩下三组的频数成公比大于2的整数等比数列,则剩下三组中频数最高的一组的频数为___________.
剖析:已知前七组的累积频率为0.79,而要研究后三组的问题,因此应先求出后三组的频率之和为1-0.79=0.21,进而求出后三组的共有频数,或者先求前七组共有频数后,再计算后三组的共有频数.
由已知知前七组的累积频数为0.79×100=79,故后三组共有的频数为21,依题意 =21,a1(1+q+q2)=21.∴a1=1,q=4.∴后三组频数最高的一组的频数为16.
=21,a1(1+q+q2)=21.∴a1=1,q=4.∴后三组频数最高的一组的频数为16.
答案:16
评述:此题剖析只按第二种思路给出了解答,你能按第一种思路来解吗?
[例4] 对某电子元件进行寿命追踪调查,情况如下:
|
寿命(h) |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
|
个 数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图和累积频率分布图;
(3)估计电子元件寿命在100-400 h以内的概率;
(4)估计电子元件寿命在400 h以上的概率.
剖析:通过本题可掌握总体分布估计的各种方法和步骤.
解:(1)频率分布表如下:
|
寿命(h) |
频 数 |
频 率 |
累积频率 |
|
100-200 |
20 |
0.10 |
0.10 |
|
200-300 |
30 |
0.15 |
0.25 |
|
300-400 |
80 |
0.40 |
0.65 |
|
400-500 |
40 |
0.20 |
0.85 |
|
500-600 |
30 |
0.15 |
1 |
|
合 计 |
200 |
1 |
|
(2)频率分布直方图如下:


(3)由累积频率分布图可以看出,寿命在100-400 h内的电子元件出现的频率为0.65,所以我们估计电子元件寿命在100-400 h内的概率为0.65.
(4)由频率分布表可知,寿命在400 h以上的电子元件出现的频率为0.20+0.15=0.35,故我们估计电子元件寿命在400 h以上的概率为0.35.
评述:画频率分布条形图、直方图时要注意纵、横坐标轴的意义.
●闯关训练
夯实基础
4.某单位有老年人27人,中年人54人,青年人81人,为了调查他们的健康状况,需从他们中抽取一个容量为36的样本,在简单随机抽样、系统抽样、分层抽样这三种方法中较合适的抽样方法是___________.
解析:要研究的总体里各部分情况差异较大,因此用分层抽样.
答案:分层抽样
3.一个容量为n的样本,分成若干组,已知某数的频数和频率分别为40、0.125,则n的值为
A.640 B.320 C.240 D.160
解析:∵ =0.125,∴n=320.故选B.
=0.125,∴n=320.故选B.
答案:B
2.一个总体中共有10个个体,用简单随机抽样的方法从中抽取一个容量为3的样本,则某特定个体入样的概率是
A. B.
B.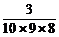 C.
C.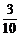 D.
D.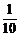
解析:用简单随机抽样法从中抽取,则每个个体被抽到的概率都相同为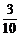 ,所以选C.
,所以选C.
答案:C
1.为调查参加运动会的1000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下列说法正确的是
A.1000名运动员是总体 B.每个运动员是个体
C.抽取的100名运动员是样本 D.样本容量是100
解析:这个问题我们研究的是运动员的年龄情况.因此应选D.
答案:D
6.总体分布:从总体中抽取一个个体,就是一次随机试验,从总体中抽取一个容量为n的样本,就是进行了n次试验,试验连同所出现的结果叫随机事件,所有这些事件的概率分布规律称为总体分布.
●点击双基
5.频率分布:用样本估计总体,是研究统计问题的基本思想方法,样本中所有数据(或数据组)的频数和样本容量的比,就是该数据的频率.所有数据(或数据组)的频率的分布变化规律叫做样本的频率分布.可以用样本频率表、样本频率分布条形图或频率分布直方图来表示.
4.总体:在数理统计中,通常把被研究的对象的全体叫做总体.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com