
2.方差反映数据的波动大小,方差越小,表示数据越稳定.
拓展题例
[例1] 如果数据a1,a2,…,a6的方差是6,那么另一组数据a1-3,a2-3,…,a6-3的方差是多少?
解:设a1,a2,…,a6的平均数为 ,则(a1-3),(a2-3),…,(a6-3)的平均数为
,则(a1-3),(a2-3),…,(a6-3)的平均数为 -3,∴方差为s2=
-3,∴方差为s2= {[(a1-3)-(
{[(a1-3)-( -3)]2+…+[(a6-3)-(
-3)]2+…+[(a6-3)-( -3)]2}=6.
-3)]2}=6.
[例2]
已知样本方差由s2=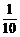
 (xi-5)2求得,求∑
(xi-5)2求得,求∑ xi.
xi.
解:依s2=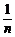 [(x1-
[(x1-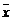 )2+…+(xn-
)2+…+(xn-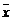 )2]
)2]
=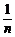 [x12+x22+…+xn2-n
[x12+x22+…+xn2-n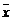 2]知,
2]知,
∴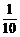
 xi=5.∴
xi=5.∴ xi=50.
xi=50.
1.期望反映数据取值的平均水平,期望越大,平均水平越高.
2.进行几次实验,得到样本数据x1,x2,…,xn,设c是任意常数,k为任意的正数,作变换yi= (xi-c)(i=1,2,…,n),则有:①
(xi-c)(i=1,2,…,n),则有:①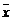 =k
=k +c;②sx2=k2sy2.
+c;②sx2=k2sy2.
●教师下载中心
教学点睛
1.用样本估计总体,除在整体上用样本的频率分布估计总体分布外,还可以用平均值和方差对总体进行估计,即用样本平均数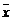 去估计总体平均数μ;用样本方差s2去估计总体的方差σ2,进一步对总体的分布作出判断.
去估计总体平均数μ;用样本方差s2去估计总体的方差σ2,进一步对总体的分布作出判断.
9.有一个容量为100的样本,数据的分组及各组的频数如下:
[12.5,15.5),6;[15.5,18.5),16;[18.5,21.5),18;[21.5,24.5),22;[24.5,27.5),20;[27.5,30.5),10;[30.5,33.5),8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计数据小于30.5的概率.
解:(1)样本的频率分布表如下:
|
分 组 |
频 数 |
频 率 |
|
12.5-15.5 |
6 |
0.06 |
|
15.5-18.5 |
16 |
0.16 |
|
18.5-21.5 |
18 |
0.18 |
|
21.5-24.5 |
22 |
0.22 |
|
24.5-27.5 |
20 |
0.20 |
|
27.5-30.5 |
10 |
0.10 |
|
30.5-33.5 |
8 |
0.08 |
|
合 计 |
100 |
1.00 |
(2)频率分布直方图如下图.

(3)数据大于等于30.5的频率是0.08,∴小于30.5的频率是0.92.∴数据小于30.5的概率约为0.92.
探究:解决总体分布估计问题的一般程序如下:(1)先确定分组的组数(最大数据与最小数据之差除组距得组数);(2)分别计算各组的频数及频率(频率= );(3)画出频率分布直方图,并作出相应的估计.
);(3)画出频率分布直方图,并作出相应的估计.
注意直方图与条形图的区别.
●思悟小结
8.甲、乙两台机床在相同的条件下同时生产一种零件,现在从中各抽测10个,它们的尺寸分别为(单位:mm):
甲:10.2 10.1 10.9 8.9 9.9 10.3 9.7 10 9.9 10.1
乙:10.3 10.4 9.6 9.9 10.1 10 9.8 9.7 10.2 10
分别计算上面两个样本的平均数与方差,如果图纸上的设计尺寸为10 mm,从计算结果看,用哪台机床加工这种零件较合适?
解: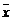 甲=
甲=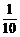 (10.2+10.1+…+10.1)=10,
(10.2+10.1+…+10.1)=10,
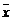 乙=
乙=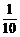 (10.3+10.4+…+10)=10,
(10.3+10.4+…+10)=10,
s甲2=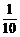 [(10.2-10)2+(10.1-10)2+…+(10.1-10)2]=0.03,
[(10.2-10)2+(10.1-10)2+…+(10.1-10)2]=0.03,
s乙2=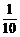 [(10.3-10)2+(10.4-10)2+…+(10-10)2]=0.06.
[(10.3-10)2+(10.4-10)2+…+(10-10)2]=0.06.
由上述结果分析,甲台机床加工这种零件稳定,较合适.
探究创新
7.某农场为了从三种不同的西红柿品种中选取高产稳定的西红柿品种,分别在五块试验田上试种,每块试验田均为0.5公顷,产量情况如下:
|
品 种 |
产量(kg) |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
21.5 |
20.4 |
22.0 |
21.2 |
19.9 |
|
2 |
21.3 |
18.9 |
18.9 |
21.4 |
19.8 |
|
3 |
17.8 |
23.3 |
21.4 |
19.1 |
20.9 |
问:哪一品种的西红柿既高产又稳定?
解: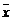 1=
1= (21.5+20.4+…+19.9)=21,
(21.5+20.4+…+19.9)=21,
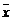 2=
2= (21.3+18.9+…+19.8)=21,
(21.3+18.9+…+19.8)=21,
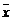 3=
3= (17.8+23.3+…+20.9)=20.5,
(17.8+23.3+…+20.9)=20.5,
s1=0.756,
s2=1.104,
s3=1.901.
由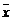 1=
1=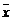 2>
2>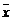 3,而s1<s2<s3,说明第1种西红柿品种既高产又稳定.
3,而s1<s2<s3,说明第1种西红柿品种既高产又稳定.
6.某校从甲、乙两名优秀选手中选拔1名参加全市中学生百米比赛,该校预先对这两名选手测试了8次,成绩如下表:
|
选手成绩(s) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
甲 |
12.1 |
12.2 |
13 |
12.5 |
13.1 |
12.5 |
12.4 |
12.2 |
|
乙 |
12 |
12.4 |
12.8 |
13 |
12.2 |
12.8 |
12.3 |
12.5 |
根据成绩,请你作出判断,派哪位选手参加更好,为什么?
解: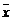 甲=12.4=
甲=12.4=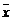 乙,s甲2=0.12,s乙2≈0.10,
乙,s甲2=0.12,s乙2≈0.10,
∴甲、乙两人的平均成绩相等,但乙的成绩较稳定,应派乙选手参加比赛.
4.为了科学地比较考试的成绩,有些选拔性考试常常会将考试分数转化为标准分,转化关系式为Z= (其中x是某位学生的考试分数,
(其中x是某位学生的考试分数,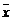 是该次考试的平均分,s是该次考试的标准差,Z称为这位学生的标准分).转化成标准分后可能出现小数和负值,因此,又常常再将Z分数作线性变换转化成其他分数.例如某次学生选拔考试采用的是T分数,线性变换公式是T=40Z+60.已知在这次考试中某位考生的考试分数是85分,这次考试的平均分是70分,标准差是25,则该考生的T分数为___________.
是该次考试的平均分,s是该次考试的标准差,Z称为这位学生的标准分).转化成标准分后可能出现小数和负值,因此,又常常再将Z分数作线性变换转化成其他分数.例如某次学生选拔考试采用的是T分数,线性变换公式是T=40Z+60.已知在这次考试中某位考生的考试分数是85分,这次考试的平均分是70分,标准差是25,则该考生的T分数为___________.
解析:由已知Z= =
= ,∴T=40×
,∴T=40× +60=24+60=84.故考生成绩的T分数为84.
+60=24+60=84.故考生成绩的T分数为84.
答案:84
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com