
9.确定抛物线方程y=x2+bx+c中的常数b和c,使得抛物线与直线y=2x在x=2处相切.
解: =2x+b,k=y′|x=2=4+b=2,
=2x+b,k=y′|x=2=4+b=2,
∴b=-2.
又当x=2时,y=22+(-2)×2+c=c,
代入y=2x,得c=4.
探究创新
8.有点难度哟!
若直线y=3x+1是曲线y=x3-a的一条切线,求实数a的值.
解:设切点为P(x0,y0),对y=x3-a求导数是
 =3x2,∴3x02=3.∴x0=±1.
=3x2,∴3x02=3.∴x0=±1.
(1)当x=1时,
∵P(x0,y0)在y=3x+1上,
∴y=3×1+1=4,即P(1,4).
又P(1,4)也在y=x3-a上,
∴4=13-a.∴a=-3.
(2)当x=-1时,
∵P(x0,y0)在y=3x+1上,
∴y=3×(-1)+1=-2,即P(-1,-2).
又P(-1,-2)也在y=x3-a上,
∴-2=(-1)3-a.∴a=1.
综上可知,实数a的值为-3或1.
7.曲线y=-x2+4x上有两点A(4,0)、B(2,4).求:
(1)割线AB的斜率kAB及AB所在直线的方程;
(2)在曲线AB上是否存在点C,使过C点的切线与AB所在直线平行?若存在,求出C点的坐标;若不存在,请说明理由.
解:(1)kAB= =-2,
=-2,
∴y=-2(x-4).
∴所求割线AB所在直线方程为2x+y-8=0.
(2) =-2x+4,-2x+4=-2,得x=3,y=-32+3×4=3.
=-2x+4,-2x+4=-2,得x=3,y=-32+3×4=3.
∴C点坐标为(3,3),所求切线方程为2x+y-9=0.
6.点P在曲线y=x3-x+ 上移动,设点P处切线的倾斜角为
上移动,设点P处切线的倾斜角为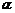 ,求
,求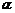 的范围.
的范围.
解:∵tan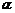 =3x2-1,
=3x2-1,
∴tan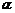 ∈[-1,+∞).
∈[-1,+∞).
当tan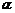 ∈[0,+∞)时,
∈[0,+∞)时,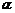 ∈[0,
∈[0, );
);
当tan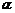 ∈[-1,0)时,
∈[-1,0)时,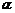 ∈[
∈[ ,π).
,π).
∴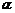 ∈[0,
∈[0, )∪[
)∪[ ,π).
,π).
培养能力
5.已知曲线y=x2-1与y=3-x3在x=x0处的切线互相垂直,求x0.
解:在x=x0处曲线y=x2-1的切线斜率为2x0,曲线y=3-x3的切线斜率为-3x02.
∵2x0·(-3x02)=-1,∴x0=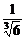 .
.
答案: 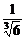
4.曲线y=2x2+1在P(-1,3)处的切线方程是________________.
解析:点P(-1,3)在曲线上,k= (-1)=-4,y-3=-4(x+1),4x+y+1=0.
(-1)=-4,y-3=-4(x+1),4x+y+1=0.
答案:4x+y+1=0
3.函数f(x)=ax3+3x2+2,若 (-1)=4,则a的值等于________.
(-1)=4,则a的值等于________.
解析:  (x)=3ax2+6x,从而使3a-6=4,∴a=
(x)=3ax2+6x,从而使3a-6=4,∴a= .
.
答案: 
2.曲线y=f(x)在点(x0,f(x0))处的切线方程为3x+y+3=0,则
A.  (x0)>0 B.
(x0)>0 B.
 (x0)<0
(x0)<0
C.  (x0)=0 D.
(x0)=0 D.
 (x0)不存在
(x0)不存在
解析:由题知 (x0)=-3.
(x0)=-3.
答案:B
1.函数f(x)=(x+1)(x2-x+1)的导数是
A.x2-x+1 B.(x+1)(2x-1)
C.3x2 D.3x2+1
解析:∵f(x)=x3+1,
∴ (x)=3x2.
(x)=3x2.
答案:C
5.设函数f(x)=(x-a)(x-b)(x-c)(a、b、c是两两不等的常数),则 +
+ +
+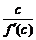 =________.
=________.
解析:∵f(x)=x3-(a+b+c)x2+(ab+bc+ca)x-abc,
∴ (x)=3x2-2(a+b+c)x+ab+bc+ca.
(x)=3x2-2(a+b+c)x+ab+bc+ca.
又 (a)=(a-b)(a-c),同理
(a)=(a-b)(a-c),同理 (b)=(b-a)(b-c),
(b)=(b-a)(b-c),
 (c)=(c-a)(c-b).
(c)=(c-a)(c-b).
代入原式中得值为0.
答案:0
●典例剖析
[例1]
(1)设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0, ],则P到曲线y=f(x)对称轴距离的取值范围为
],则P到曲线y=f(x)对称轴距离的取值范围为
A.[0,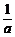 ]
B.[0,
]
B.[0,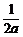 ] C.[0,|
] C.[0,| |] D.[0,|
|] D.[0,|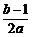 |]
|]
(2)(2004年全国,3)曲线y=x3-3x2+1在点(1,-1)处的切线方程为
A.y=3x-4 B.y=-3x+2 C.y=-4x+3 D.y=4x-5
(3)(2004年重庆,15)已知曲线y= x3+
x3+ ,则过点P(2,4)的切线方程是______.
,则过点P(2,4)的切线方程是______.
(4)(2004年湖南,13)过点P(-1,2)且与曲线y=3x2-4x+2在点M(1,1)处的切线平行的直线方程是______.
剖析:本题的各小题都是考查导数的几何意义的,导数的几何意义是曲线在该点处的切线的斜率.
解析:(1)∵过P(x0,f(x0))的切线的倾斜角的取值范围是[0, ],
],
∴P到曲线y=f(x)对称轴x=- 的距离d=x0-(-
的距离d=x0-(- )=x0+
)=x0+ .
.
又∵ (x0)=2ax0+b∈[0,1],
(x0)=2ax0+b∈[0,1],
∴x0∈[ ,
,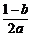 ].∴d=x0+
].∴d=x0+ ∈[0,
∈[0,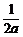 ].
].
(2)∵点(1,-1)在曲线上,y′=3x2-6x,
∴切线斜率为3×12-6×1=-3.
∴所求切线方程为y+1=-3(x-1).
(3)∵P(2,4)在y= x3+
x3+ 上,
上,
又y′=x2,∴斜率k=22=4.
∴所求直线方程为y-4=4(x-2),4x-y-4=0.
(4)y′=6x-4,∴切线斜率为6×1-4=2.
∴所求直线方程为y-2=2(x+1),即2x-y+4=0.
答案:(1)B (2)B (3)4x-y-4=0 (4)2x-y+4=0
评述:利用导数的几何意义,求切线的斜率是导数的一个基本应用.
思考讨论
导数除用来求切线的斜率外,还有哪些方面的应用?
答:导数的应用较广,如求函数的单调区间,求函数的极值、最值等.
[例2] 曲线y=x3在点(3,27)处的切线与两坐标轴所围成的三角形面积是多少?
剖析:求出切线的方程后再求切线与坐标轴的交点.
解:曲线在点(3,27)处切线的方程为y=27x-54,此直线与x轴、y轴交点分别为(2,0)和(0,-54),
∴切线与坐标轴围成的三角形面积是S=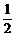 ×2×54=54.
×2×54=54.
评述:求切线的斜率是导数的一个基本应用.
[例3] 已知曲线C:y=x3-3x2+2x,直线l:y=kx,且直线l与曲线C相切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标.
剖析:切点(x0,y0)既在曲线上,又在切线上,由导数可得切线的斜率.联立方程组解之即可.
解:∵直线过原点,则k= (x0≠1).
(x0≠1).
由点(x0,y0)在曲线C上,则y0=x03-3x02+2x0,
∴ =x02-3x0+2.
=x02-3x0+2.
又y′=3x2-6x+2,
∴在(x0,y0)处曲线C的切线斜率应为k= (x0)=3x02-6x0+2.
(x0)=3x02-6x0+2.
∴x02-3x0+2=3x02-6x0+2.
整理得2x02-3x0=0.
解得x0=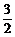 (∵x0≠0).
(∵x0≠0).
这时,y0=-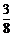 ,k=-
,k=- .
.
因此,直线l的方程为y=- x,切点坐标是(
x,切点坐标是(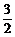 ,-
,-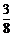 ).
).
评述:对于高次函数凡涉及到切线或其单调性的问题时,要有求导意识.
[例4] 证明:过抛物线y=a(x-x1)·(x-x2)(a≠0,x1<x2)上两点A(x1,0)、B(x2,0)的切线,与x轴所成的锐角相等.
剖析:利用与x轴所成的锐角和倾斜角之间的关系,只要求出切线的斜率进行比较即可.
解:y′=2ax-a(x1+x2),
y′|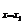 =a(x1-x2),即kA=a(x1-x2),y′|
=a(x1-x2),即kA=a(x1-x2),y′| =a(x2-x1),即kB=a(x2-x1).
=a(x2-x1),即kB=a(x2-x1).
设两条切线与x轴所成的锐角为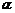 、β,则tan
、β,则tan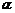 =|kA|=|a(x1-x2)|,
=|kA|=|a(x1-x2)|,
tanβ=|kB|=|a(x2-x1)|,故tan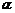 =tanβ.
=tanβ.
又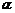 、β是锐角,则
、β是锐角,则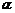 =β.
=β.
评述:由tan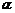 =tanβ不能直接得
=tanβ不能直接得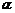 =β,还必须有
=β,还必须有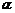 、β为锐角时(或在同一单调区间上时)才能得
、β为锐角时(或在同一单调区间上时)才能得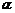 =β.
=β.
●闯关训练
夯实基础
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com