
2.某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是
A.10% B.15% C.18% D.20%
解析:设降价百分率为x%,
∴2000(1-x%)2=1280.解得x=20.
答案:D
1.设集合A和B都是自然数集合N,映射f:A→B把集合A中的元素n映射到集合B中的元素2n+n,则在映射f下,象20的原象是
A.2 B.3 C.4 D.5
解析:由2n+n=20求n,用代入法可知选C.
答案:C
5.(2004年浙江,文9)若函数f(x)=loga(x+1)(a>0,a≠1)的定义域和值域都是[0,1],则a等于
A.  B.
B.
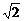 C.
C. D.2
D.2
解析:f(x)=loga(x+1)的定义域是[0,1],∴0≤x≤1,则1≤x+1≤2.
当a>1时,0=loga1≤loga(x+1)≤loga2=1,∴a=2;
当0<a<1时,loga2≤loga(x+1)≤loga1=0,与值域是[0,1]矛盾.
综上,a=2.
答案:D
●典例剖析
[例1] 试判断以下各组函数是否表示同一函数?
(1)f(x)=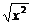 ,g(x)=
,g(x)= ;
;
(2)f(x)= ,g(x)=
,g(x)=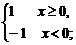
(3)f(x)=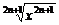 ,g(x)=(
,g(x)=(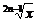 )2n-1(n∈N*);
)2n-1(n∈N*);
(4)f(x)=
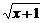 ,g(x)=
,g(x)= ;
;
(5)f(x)=x2-2x-1,g(t)=t2-2t-1.
剖析:对于两个函数y=f(x)和y=g(x),当且仅当它们的定义域、值域、对应法则都相同时,y=f(x)和y=g(x)才表示同一函数.若两个函数表示同一函数,则它们的图象完全相同,反之亦然.
解:(1)由于f(x)=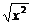 =|x|,g(x)=
=|x|,g(x)= =x,故它们的值域及对应法则都不相同,所以它们不是同一函数.
=x,故它们的值域及对应法则都不相同,所以它们不是同一函数.
(2)由于函数f(x)= 的定义域为(-∞,0)∪(0,+∞),而g(x)=
的定义域为(-∞,0)∪(0,+∞),而g(x)=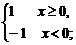 的定义域为R,所以它们不是同一函数.
的定义域为R,所以它们不是同一函数.
(3)由于当n∈N*时,2n±1为奇数,∴f(x)=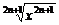 =x,g(x)=(
=x,g(x)=(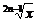 )2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数.
)2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数.
(4)由于函数f(x)=
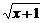 的定义域为{x|x≥0},而g(x)=
的定义域为{x|x≥0},而g(x)= 的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数.
的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数.
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数.
评述:(1)第(5)小题易错判断成它们是不同的函数,原因是对函数的概念理解不透.要知道,在函数的定义域及对应法则f不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f(x)=x2+1,f(t)=t2+1,f(u+1)=(u+1)2+1都可视为同一函数.
(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数.
[例2] 集合A={3,4},B={5,6,7},那么可建立从A到B的映射个数是__________,从B到A的映射个数是__________.
剖析:从A到B可分两步进行:第一步A中的元素3可有3种对应方法(可对应5或6或7),第二步A中的元素4也有这3种对应方法.由乘法原理,不同的映射种数N1=3×3=9.反之从B到A,道理相同,有N2=2×2×2=8种不同映射.
答案:9 8
深化拓展
设集合A中含有4个元素,B中含有3个元素,现建立从A到B的映射f:A→B,且使B中每个元素在A中都有原象,则这样的映射有___________________个.
提示:因为集合A中有4个元素,集合B中有3个元素,根据题意,A中必须有2个元素有同一个象,因此,共有C A
A =36个映射.
=36个映射.
答案:36
[例3] (2004年广东,19)设函数f(x)=|1- |(x>0),证明:当0<a<b,且f(a)=f(b)时,ab>1.
|(x>0),证明:当0<a<b,且f(a)=f(b)时,ab>1.
剖析一:f(a)=f(b) |1-
|1- |=|1-
|=|1-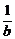 |
| (1-
(1- )2=(1-
)2=(1-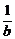 )2
)2 2ab=a+b≥2
2ab=a+b≥2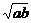
 ab>1.
ab>1.
证明:略.
剖析二:f(x)=
证明:f(x)在(0,1]上是减函数,在(1,+∞)上是增函数.由0<a<b且f(a)= f(b),得0<a<1<b且 -1=1-
-1=1-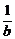 ,即
,即 +
+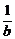 =2
=2 a+b=2ab≥2
a+b=2ab≥2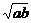
 ab>1.
ab>1.
评注:证法一、证法二是去绝对值符号的两种基本方法.
●闯关训练
夯实基础
4.(2004年全国Ⅲ,理5)函数y=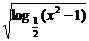 的定义域是
的定义域是
A.[-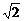 ,-1)∪(1,
,-1)∪(1,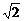 ] B.(-
] B.(- ,-1)∪(1,
,-1)∪(1,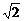 )
)
C.[-2,-1)∪(1,2] D.(-2,-1)∪(1,2)
解析: -
-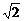 ≤x<-1或1<x≤
≤x<-1或1<x≤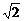 .
.
∴y=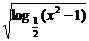 的定义域为[-
的定义域为[-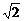 ,-1)∪(1,
,-1)∪(1,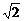 ].
].
答案:A
3.(2004年全国Ⅰ,理2)已知函数f(x)=lg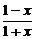 ,若f(a)=b,则f(-a)等于
,若f(a)=b,则f(-a)等于
A.b B.-b C.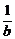 D.-
D.-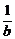
解析:f(-a)=lg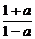 =-lg
=-lg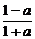 =-f(a)=-b.
=-f(a)=-b.
[答案] B
2.设M={x|-2≤x≤2},N={y|0≤y≤2},函数f(x)的定义域为M,值域为N,则f(x)的图象可以是
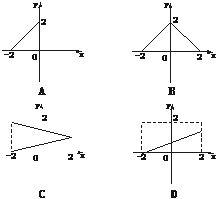
解析:A项定义域为[-2,0],D项值域不是[0,2],C项对任一x都有两个y与之对应,都不符.故选B.
答案:B
1.设集合A=R,集合B=正实数集,则从集合A到集合B的映射f只可能是
A.f:x→y=|x| B.f:x→y=
C.f:x→y=3-x D.f:x→y=log2(1+|x|)
解析:指数函数的定义域是R,值域是(0,+∞),所以f是x→y=3-x.
答案:C
3.映射的定义:一般地,设A、B是两个集合,如果按照某种对应关系f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,那么,这样的对应(包括集合A、B,以及集合A到集合B的对应关系f)叫做集合A到集合B的映射,记作f:A→B.
由映射和函数的定义可知,函数是一类特殊的映射,它要求A、B非空且皆为数集.
特别提示
函数定义的三要素是理解函数概念的关键,用映射的观点理解函数概念是对函数概念的深化.
●点击双基
2.两个函数的相等:函数的定义含有三个要素,即定义域A、值域C和对应法则f.当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定.因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数.
1.函数的定义:设A、B是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中x叫做自变量.x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com