
3.函数的定义域是构成函数的非常重要的部分,如没有标明定义域,则认为定义域为使得函数解析式有意义的x的取值范围,即分式中分母应不等于0;偶次根式中被开方数应为非负数;零指数幂中,底数不等于0,负分数指数幂中,底数应大于0;对数式中,真数必须大于0,底数必须大于0且不等于1……实际问题中还需考虑自变量的实际意义.若解析式由几个部分组成,则定义域为各个部分相应集合的交集.
●教师下载中心
教学点睛
2.理解映射的概念,应注意以下几点:
(1)集合A、B及对应法则f是确定的,是一个系统;
(2)对应法则有“方向性”,即强调从集合A到集合B的对应,它与从集合B到集合A的对应关系一般是不同的;
(3)集合A中每一个元素,在集合B中都有象,并且象是唯一的,这是映射区别于一般对应的本质特征;
(4)集合A中不同元素,在集合B中对应的象可以是同一个;
(5)不要求集合B中的每一个元素在集合A中都有原象.
1.本节重点内容是函数概念、定义域、值域,难点是映射及其意义.
9.集合M={a,b,c},N={-1,0,1},映射f:M→N满足f(a)+f(b)+f(c)=0,那么映射f:M→N的个数是多少?
解:∵f(a)∈N,f(b)∈N,f(c)∈N,且f(a)+f(b)+f(c)=0,
∴有0+0+0=0+1+(-1)=0.
当f(a)=f(b)=f(c)=0时,只有一个映射;
当f(a)、f(b)、f(c)中恰有一个为0,而另两个分别为1,-1时,有C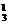 ·A
·A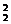 =6个映射.因此所求的映射的个数为1+6=7.
=6个映射.因此所求的映射的个数为1+6=7.
评述:本题考查了映射的概念和分类讨论的思想.
●思悟小结
8.如果函数f(x)=(x+a)3对任意x∈R都有f(1+x)=-f(1-x),试求f(2)+ f(-2)的值.
解:∵对任意x∈R,总有f(1+x)=-f(1-x),
∴当x=0时应有f(1+0)=-f(1-0),
即f(1)=-f(1).∴f(1)=0.
又∵f(x)=(x+a)3,∴f(1)=(1+a)3.
故有(1+a)3=0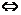 a=-1.∴f(x)=(x-1)3.
a=-1.∴f(x)=(x-1)3.
∴f(2)+f(-2)=(2-1)3+(-2-1)3=13+(-3)3=-26.
探究创新
7.若f :y=3x+1是从集合A={1,2,3,k}到集合B={4,7,a4,a2+3a}的一个映射,求自然数a、k的值及集合A、B.
解:∵f(1)=3×1+1=4,f(2)=3×2+1=7,f(3)=3×3+1=10,f(k)=3k+1,由映射的定义知
(1)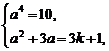 或(2)
或(2)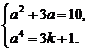
∵a∈N,∴方程组(1)无解.
解方程组(2),得a=2或a=-5(舍),3k+1=16,3k=15,k=5.∴A={1,2,3,5},B={4,7,10,16}.
6.如下图,在边长为4的正方形ABCD上有一点P,沿着折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).
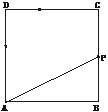
(1)求△ABP的面积与P移动的路程间的函数关系式;
(2)作出函数的图象,并根据图象求y的最大值.
解:(1)这个函数的定义域为(0,12).
当0<x≤4时,S=f(x)=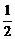 ·4·x=2x;
·4·x=2x;
当4<x≤8时,S=f(x)=8;
当8<x<12时,S=f(x)=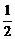 ·4·(12-x)=2(12-x)=24-2x.
·4·(12-x)=2(12-x)=24-2x.
∴这个函数的解析式为
f(x)=
(2)其图形为 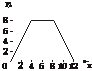
由图知,[f(x)]max=8.
5.(2004年全国Ⅳ,文)已知函数y=log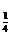 x与y=kx的图象有公共点A,且A点的横坐标为2,则k的值等于
x与y=kx的图象有公共点A,且A点的横坐标为2,则k的值等于
A.-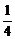 B.
B.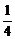 C.-
C.-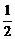 D.
D.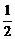
解析:由点A在y=log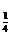 x的图象上可求出A点纵坐标y=log
x的图象上可求出A点纵坐标y=log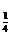 2=-
2=-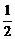 .又A(2,-
.又A(2,-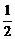 )在y=kx图象上,-
)在y=kx图象上,-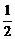 =k·2,∴k=-
=k·2,∴k=-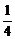 .
.
答案:A
培养能力
4.(2004年浙江,文13)已知f(x)=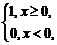 则不等式xf(x)+x≤2的解集是___________________.
则不等式xf(x)+x≤2的解集是___________________.
解析:x≥0时,f(x)=1,
xf(x)+x≤2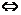 x≤1,∴0≤x≤1;
x≤1,∴0≤x≤1;
当x<0时,f(x)=0,
xf(x)+x≤2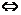 x≤2,∴x<0.综上x≤1.
x≤2,∴x<0.综上x≤1.
答案:{x|x≤1}
3.(2004年全国Ⅲ,理11)设函数f(x)=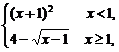 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
解析:f(x)是分段函数,故f(x)≥1应分段求解.
当x<1时,f(x)≥1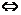 (x+1)2≥1
(x+1)2≥1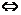 x≤-2或x≥0,∴x≤-2或0≤x<1.
x≤-2或x≥0,∴x≤-2或0≤x<1.
当x≥1时,f(x)≥1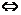 4-
4-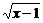 ≥1
≥1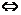
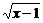 ≤3
≤3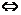 x≤10,∴1≤x≤10.
x≤10,∴1≤x≤10.
综上所述,x≤-2或0≤x≤10.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com