
2.函数单调性可以从三个方面理解
(1)图形刻画:对于给定区间上的函数f(x),函数图象如从左向右连续上升,则称函数在该区间上单调递增,函数图象如从左向右连续下降,则称函数在该区间上单调递减.
(2)定性刻画:对于给定区间上的函数f(x),如函数值随自变量的增大而增大,则称函数在该区间上单调递增,如函数值随自变量的增大而减小,则称函数在该区间上单调递减.
(3)定量刻画,即定义.
上述三方面是我们研究函数单调性的基本途径.
●点击双基
1.增函数、减函数的定义
一般地,对于给定区间上的函数f(x),如果对于属于这个区间的任意两个自变量的值x1、x2,当x1<x2时,都有f(x1)<f(x2)(或都有f(x1)>f(x2)),那么就说f(x)在这个区间上是增函数(或减函数).
如果函数y=f(x)在某个区间上是增函数(或减函数),就说f(x)在这一区间上具有(严格的)单调性,这一区间叫做f(x)的单调区间.如函数是增函数则称区间为增区间,如函数为减函数则称区间为减区间.
2.3函数的单调性
●知识梳理
3.新课改对函数的图象表示提出了更高的要求,要加强图象表示的教学.
拓展题例
[例题] 已知扇形的周长为10,求扇形半径r与面积S的函数关系式及此函数的定义域、值域.
解:设扇形的弧长为l,则l=10-2r,
∴S= lr=(5-r)r=-r2+5r.
lr=(5-r)r=-r2+5r.
由
得 <r<5.
<r<5.
∴S=-r2+5r的定义域为( ,5).
,5).
又S=-r2+5r=-(r-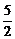 )2+
)2+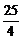 且
且
r=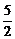 ∈(
∈( ,π),
,π),
∴当r=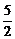 时,S最大=
时,S最大=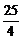 .
.
又S>-52+5×5=0,
∴S=-r2+5r,r∈( ,5)的值域为(0,
,5)的值域为(0,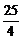 ].
].
2.强化待定系数法在求函数解析式中的重要作用.
1.用换元法解决问题时,应提醒学生注意“新元”相应的取值范围.
3.要熟悉求函数值域的几种基本方法,遇到求值域的问题,应优先考虑采用特殊方法,如不等式法、配方法、几何法、换元法等.当特殊方法不易解决时,再采用一般方法如方程法求解.如一题可有多种方法解决时,应注意选择最优解法.
●教师下载中心
教学点睛
2.求函数解析式的方法一般有待定系数法和换元法.如果已知函数式的构造模式,可用待定系数法;如果已知复合函数f[g(x)]的表达式来求f(x),常用换元法;当已知表达式较简单时,甚至可直接用凑配法求解.
1.并不是所有的函数关系都可以用解析式来表示,函数还有另外两种表示方法:列表法、图象法.
9.图①是某公共汽车线路收支差额y元与乘客量x的图象.

(1)试说明图①上点A、点B以及射线AB上的点的实际意义.
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图②③所示.你能根据图象,说明这两种建议的意义吗?
解:(1)点A表示无人乘车时收入差额为-20元,点B表示有10人乘车时收入差额为0元,线段AB上的点表示亏损,AB延长线上的点表示赢利.
(2)图②的建议是降低成本,票价不变,图③的建议是增加票价.
深化拓展
(1)图①、图②中的票价是多少元?图③中的票价是多少元?
(2)此问题中直线斜率的实际意义是什么?
答案:(1)图①②中的票价是2元.
图(3)中的票价是4元.
(2)斜率表示票价.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com