2.4　 函数的奇偶性

●知识梳理

3.讨论复合函数单调性的根据：设y=f(u)，u=g(x)，x∈［a，b］，u∈［m，n］都是单调函数，则y=f［g(x)］在［a，b］上也是单调函数.

(1)若y=f(u)是［m，n］上的增函数，则y=f［g(x)］与u=g(x)的增减性相同；

(2)若y=f(u)是［m，n］上的减函数，则y=f［g(x)］的增减性与u=g(x)的增减性相反.

拓展题例

[例1] 设函数f(x)＝(a＞b＞0)，求f(x)的单调区间，并证明f(x)在其单调区间上的单调性.

解：函数f(x)＝的定义域为(－∞，－b)∪(－b，+∞)，

任取x₁、x₂∈(－∞，－b)且x₁＜x₂，

则f(x₁)－f(x₂)＝－＝.

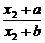∵a－b＞0，x₂－x₁＞0，(x₁+b)(x₂+b)＞0，

∴f(x₁)－f(x₂)＞0，

即f(x)在(－∞，－b)上是减函数.

同理可证f(x)在(－b，+∞)上也是减函数.

∴函数f(x)=在(－∞，－b)与(－b，+∞)上均为减函数.

[例2] 已知f(x)是定义在［－1，1］上的奇函数，且f(1)=1，若a、b∈［－1，1］，a+b≠0时，有＞0.

判断函数f(x)在［－1，1］上是增函数还是减函数，并证明你的结论.

解：任取x₁、x₂∈［－1，1］，且x₁＜x₂，则－x₂∈［－1，1］.又f(x)是奇函数，于是

f(x₁)－f(x₂)=f(x₁)+f(－x₂)

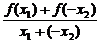=·(x₁－x₂).

据已知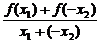＞0，x₁－x₂＜0，

∴f(x₁)－f(x₂)＜0，即f(x₁)＜f(x₂).

∴f(x)在［－1，1］上是增函数.

2.教学过程中应要求学生准确理解、把握单调性定义中“任意”的含意，函数单调性的重要作用在于化归，要重视运用函数的单调性将问题化归转化，培养化归意识.

1.本节的重点是函数单调性的有关概念，难点是利用概念证明或判断函数的单调性.复习本节时，老师最好引导学生总结出证明函数单调性的一般步骤：1°设值；2°作差；3°变形；4°定号；5°结论.

4.讨论函数的单调性必须在定义域内进行.

●教师下载中心

教学点睛

3.在解决与函数单调性有关的问题时，通常有定义法、图象法、复合函数判断法，但最基本的方法是定义法，几乎所有的与单调性有关的问题都可用定义法来解决.

2.函数单调性定义中的x₁、x₂有三个特征：一是同属一个单调区间；二是任意性，即x₁、x₂是给定区间上的任意两个值，“任意”二字绝不能丢掉，更不可随意以两个特殊值替换；三是有大小，通常规定x₁＜x₂.三者缺一不可.

1.函数的单调性是对于函数定义域内的某个子区间而言的.有些函数在整个定义域内是单调的，如一次函数；而有些函数在定义域内的部分区间上是增函数而在另一部分区间上可能是减函数，如二次函数；还有的函数是非单调的，如y=

8.(2005年北京西城区模拟题)设a∈R，函数f(x)=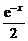(ax²+a+1)，其中e是自然对数的底数.

(1)判断f(x)在R上的单调性；

(2)当－1＜a＜0时，求f(x)在［1，2］上的最小值.

解：(1)由已知

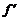(x)=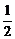－e^－x(ax²+a+1)+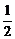e^－x·2ax

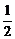=e^－x(－ax²+2ax－a－1).

因为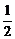e^－x＞0，以下讨论函数g(x)=－ax²+2ax－a－1值的情况：

当a=0时，g(x)=－1＜0，即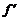(x)＜0，所以f(x)在R上是减函数.

当a＞0时，g(x)=0的判别式Δ=4a²－4(a²+a)=－4a＜0，所以g(x)＜0，即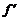(x)＜0，所以f(x)在R上是减函数.

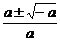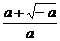当a＜0时，g(x)=0有两个根x_1，2=，并且＜，所以在区间(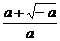－∞，)上，g(x)＞0，即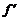(x)＞0，f(x)在此区间上是增函数；

在区间(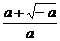，)上，g(x)＜0，即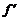(x)＜0，f(x)在此区间上是减函数.

在区间(，+∞)上，g(x)＞0，即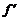(x)＞0，f(x)在此区间上是增函数.

综上，当a≥0时，f(x)在R上是减函数；

当a＜0时，f(x)在(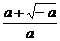－∞，)上单调递增，在(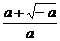，)上单调递减，在(，+∞)上单调递增.

(2)当－1＜a＜0时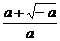，=1+＜1，=1+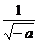＞2，所以在区间［1，2］上，函数f(x)单调递减.所以函数f(x)在区间［1，2］上的最小值为f(2)=.

评述：函数的最值和函数的单调性有紧密联系.判断较复杂函数的单调性，利用导函数的符号是基本方法.

●思悟小结

7.(2004年春季上海)已知函数f(x)=|x－a|，g(x)=x²+2ax+1(a为正常数)，且函数f(x)与g(x)的图象在y轴上的截距相等.

(1)求a的值；

(2)求函数f(x)+g(x)的单调递增区间；

(3)若n为正整数，证明10^f(n)·()^g(n)＜4.

(1)解：由题意，f(0)=g(0)，|a|=1，又a＞0，所以a=1.

(2)解：f(x)+g(x)=|x－1|+x²+2x+1.

当x≥1时，f(x)+g(x)=x²+3x，它在［1，+∞)上单调递增；

当x＜1时，f(x)+g(x)=x²+x+2，它在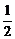［－，1)上单调递增.

(3)证明：设c_n=10^f(n)·()^g(n)，考查数列{c_n}的变化规律：

解不等式＜1，由c_n＞0，上式化为

10·()²ⁿ⁺³＜1，

解得n＞－≈3.7.因n∈N^*，得n≥4，于是c₁≤c₂≤c₃≤c₄.而c₄＞c₅＞c₆＞…，

所以10^f(n)·()^g(n)≤10^f(4)·()^g(4)=10³·()²⁵＜4.

探究创新