
4.满足条件m >(mm)2的正数m的取值范围是___________________.
>(mm)2的正数m的取值范围是___________________.
解析:∵m>0,∴当m>1时,有m2>2m,即m>2;
当0<m<1时,有m2<2m,即0<m<1.
综上所述,m>2或0<m<1.
答案:m>2或0<m<1
3.化简 (a>0,b>0)的结果是___________________.
(a>0,b>0)的结果是___________________.
解析:原式= =
=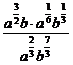 =
=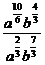 =
= .
.
答案:
2.下列函数中值域为正实数的是
A.y=-5x B.y=( )1-x
)1-x
C.y= D.y=
D.y=
解析:∵y=( )x的值域是正实数,而1-x∈R,∴y=(
)x的值域是正实数,而1-x∈R,∴y=( )1-x的值域是正实数.
)1-x的值域是正实数.
答案:B
1.已知f(x)=ax,g(x)=-logbx,且lga+lgb=0,a≠1,b≠1,则y=f(x)与y=g(x)的图象
A.关于直线x+y=0对称 B.关于直线x-y=0对称
C.关于y轴对称 D.关于原点对称
解析:lga+lgb=0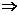 ab=1.
ab=1.
∴g(x)=-logbx=-loga-1x=logax.
∴f(x)与g(x)的图象关于y=x对称.
答案:B
6.函数y=( )
)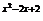 的递增区间是___________.
的递增区间是___________.
解析:∵y=( )x在(-∞,+∞)上是减函数,而函数y=x2-2x+2=(x-1)2+1的递减区间是(-∞,1],∴原函数的递增区间是(-∞,1].
)x在(-∞,+∞)上是减函数,而函数y=x2-2x+2=(x-1)2+1的递减区间是(-∞,1],∴原函数的递增区间是(-∞,1].
答案:(-∞,1]
●典例剖析
[例1] 下图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图象,则a、b、c、d与1的大小关系是

A.a<b<1<c<d B.b<a<1<d<c
C.1<a<b<c<d D.a<b<1<d<c
剖析:可先分两类,即(3)(4)的底数一定大于1,(1)(2)的底数小于1,然后再从(3)(4)中比较c、d的大小,从(1)(2)中比较a、b的大小.
解法一:当指数函数底数大于1时,图象上升,且当底数越大,图象向上越靠近于y轴;当底数大于0小于1时,图象下降,底数越小,图象向右越靠近于x轴.得b<a<1<d<c.
解法二:令x=1,由图知c1>d1>a1>b1,
∴b<a<1<d<c.
答案:B
[例2] 已知2 ≤(
≤(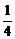 )x-2,求函数y=2x-2-x的值域.
)x-2,求函数y=2x-2-x的值域.
解:∵2 ≤2-2(x-2),∴x2+x≤4-2x,即x2+3x-4≤0,得-4≤x≤1.又∵y=2x-2-x是[-4,1]上的增函数,∴2-4-24≤y≤2-2-1.故所求函数y的值域是[-
≤2-2(x-2),∴x2+x≤4-2x,即x2+3x-4≤0,得-4≤x≤1.又∵y=2x-2-x是[-4,1]上的增函数,∴2-4-24≤y≤2-2-1.故所求函数y的值域是[- ,
, ].
].
[例3] 要使函数y=1+2x+4xa在x∈(-∞,1]上y>0恒成立,求a的取值范围.
解:由题意,得1+2x+4xa>0在x∈(-∞,1]上恒成立,即a>- 在x∈(-∞,1]上恒成立.又∵-
在x∈(-∞,1]上恒成立.又∵- =-(
=-( )2x-(
)2x-( )x=-[(
)x=-[( )x+
)x+ ]2+
]2+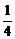 ,当x∈(-∞,1]时值域为(-∞,-
,当x∈(-∞,1]时值域为(-∞,- ],∴a>-
],∴a>- .
.
评述:将不等式恒成立问题转化为求函数值域问题是解决这类问题常用的方法.
●闯关训练
夯实基础
5.(2004年湖南,文16)若直线y=2a与函数y=|ax-1|(a>0且a≠1)的图象有两个公共点,则a的取值范围是___________________.
解析:数形结合.由图象可知0<2a<1,0<a< .
.
答案:0<a<
4.(2004年全国Ⅱ,理6)函数y=-ex的图象
A.与y=ex的图象关于y轴对称 B.与y=ex的图象关于坐标原点对称
C.与y=e-x的图象关于y轴对称 D.与y=e-x的图象关于坐标原点对称
解析:图象法.
答案:D
3.(2004年湖北,文5)若函数y=ax+b-1(a>0且a≠1)的图象经过二、三、四象限,则一定有
A.0<a<1且b>0 B.a>1且b>0
C.0<a<1且b<0 D.a>1且b<0
解析:作函数y=ax+b-1的图象.
答案:C
2.(2003年郑州市质量检测题)函数y=2 的图象与直线y=x的位置关系是
的图象与直线y=x的位置关系是

解析:y=2 =(
=( )x.
)x.
∵ >1,∴不可能选D.
>1,∴不可能选D.
又∵当x=1时,2 >x,而当x=3时,2
>x,而当x=3时,2 <x,∴不可能选A、B.
<x,∴不可能选A、B.
答案:C
1. ·
· 等于
等于
A.- B.-
B.-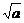
C. D.
D.
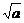
解析: ·
· =a
=a ·(-a)
·(-a) =-(-a)
=-(-a) =-(-a)
=-(-a) .
.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com