
3.在给定条件下,求字母的取值范围是常见题型,要重视不等式知识及函数单调性在这类问题上的应用.
●教师下载中心
教学点睛
2.比较几个数的大小是对数函数性质应用的常见题型.在具体比较时,可以首先将它们与零比较,分出正负;正数通常都再与1比较分出大于1还是小于1,然后在各类中间两两相比较.
1.对数的底数和真数应满足的条件是求解对数问题时必须予以特别重视的.
9.(2004年苏州市模拟题)已知函数f(x)=3x+k(k为常数),A(-2k,2)是函数y= f -1(x)图象上的点.
(1)求实数k的值及函数f -1(x)的解析式;
(2)将y= f -1(x)的图象按向量a=(3,0)平移,得到函数y=g(x)的图象,若2 f -1(x+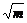 -3)-g(x)≥1恒成立,试求实数m的取值范围.
-3)-g(x)≥1恒成立,试求实数m的取值范围.
解:(1)∵A(-2k,2)是函数y= f -1(x)图象上的点,
∴B(2,-2k)是函数y=f(x)上的点.
∴-2k=32+k.∴k=-3.
∴f(x)=3x-3.
∴y= f -1(x)=log3(x+3)(x>-3).
(2)将y= f -1(x)的图象按向量a=(3,0)平移,得到函数y=g(x)=log3x(x>0),要使2 f -1(x+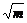 -3)-g(x)≥1恒成立,即使2log3(x+
-3)-g(x)≥1恒成立,即使2log3(x+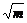 )-log3x≥1恒成立,所以有x+
)-log3x≥1恒成立,所以有x+ +2
+2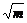 ≥3在x>0时恒成立,只要(x+
≥3在x>0时恒成立,只要(x+ +2
+2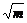 )min≥3.
)min≥3.
又x+ ≥2
≥2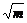 (当且仅当x=
(当且仅当x= ,即x=
,即x=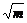 时等号成立),∴(x+
时等号成立),∴(x+ +2
+2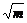 )min=4
)min=4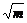 ,即4
,即4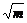 ≥3.∴m≥
≥3.∴m≥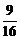 .
.
●思悟小结
8.若f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1).
(1)求f(log2x)的最小值及对应的x值;
(2)x取何值时,f(log2x)>f(1)且log2[f(x)]<f(1)?
解:(1)∵f(x)=x2-x+b,
∴f(log2a)=log22a-log2a+b.
由已知有log22a-log2a+b=b,
∴(log2a-1)log2a=0.
∵a≠1,∴log2a=1.∴a=2.
又log2[f(a)]=2,∴f(a)=4.
∴a2-a+b=4,b=4-a2+a=2.
故f(x)=x2-x+2,从而f(log2x)=log22x-log2x+2=(log2x- )2+
)2+ .
.
∴当log2x= 即x=
即x=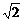 时,f(log2x)有最小值
时,f(log2x)有最小值 .
.
(2)由题意
 0<x<1.
0<x<1.
探究创新
7.函数f(x)=log2|x|,g(x)=-x2+2,则f(x)·g(x)的图象只可能是

解析:∵f(x)与g(x)都是偶函数,∴f(x)·g(x)也是偶函数,由此可排除A、D.
又由x→+∞时,f(x)·g(x)→-∞,可排除B.
答案:C
6.设函数f(x)=lg(1-x),g(x)=lg(1+x),在f(x)和g(x)的公共定义域内比较|f(x)|与|g(x)|的大小.
解:f(x)、g(x)的公共定义域为(-1,1).
|f(x)|-|g(x)|=|lg(1-x)|-|lg(1+x)|.
(1)当0<x<1时,|lg(1-x)|-|lg(1+x)|=-lg(1-x2)>0;
(2)当x=0时,|lg(1-x)|-|lg(1+x)|=0;
(3)当-1<x<0时,|lg(1-x)|-|lg(1+x)|=lg(1-x2)<0.
综上所述,当0<x<1时,|f(x)|>|g(x)|;当x=0时,|f(x)|=|g(x)|;当-1<
x<0时,|f(x)|<|g(x)|.
培养能力
5.已知y=loga(3-ax)在[0,2]上是x的减函数,求a的取值范围.
解:∵a>0且a≠1,∴t=3-ax为减函数.依题意a>1,又t=3-ax在[0,2]上应有t>0,∴3-2a>0.∴a< .故1<a<
.故1<a< .
.
4.(2004年春季上海)方程lgx+lg(x+3)=1的解x=___________________.
解析:由lgx+lg(x+3)=1,得x(x+3)=10,x2+3x-10=0.
∴x=-5或x=2.
∵x>0,∴x=2.
答案:2
3.(2004年湖南,理3)设f -1(x)是f(x)=log2(x+1)的反函数,若[1+ f -1(a)][1+ f -1(b)]=8,则f(a+b)的值为
A.1 B.2 C.3 D.log23
解析:∵f -1(x)=2x-1,∴[1+ f -1(a)][1+ f -1(b)]=2a·2b=2a+b.由已知2a+b=8,∴a+b=3.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com